Maths

Statistics

Statistics is a branch of mathematics dealing with data collection, analysis, interpretation, and presentation. It provides tools for making informed decisions based on data.

Key Concepts

Descriptive Statistics: Summarizes data using measures like mean, median, mode, and standard deviation.
Inferential Statistics: Makes predictions or inferences about a population based on a sample of data.

Population vs Sample

Population 📊
- Complete dataset
- Example: All students in a university
- N = Total size
Sample 🔍
- Subset of population
- Example: 100 randomly selected students
- n = Sample size

Key Point: Sample should be representative of the population

Measures of Central Tendency

Measures of Central Tendency are used to describe the central or typical value of a dataset.
Mean:
- Average of all values in a dataset
- Sample Formula: x̄ = (∑x) / n
- Population Formula: μ = (∑x) / N
- Example: For [2,4,6,8], Mean = (2+4+6+8)/4 = 5
- Use when:
  - Data is normally distributed
  - Need a value affected by all data points
- Limitations:
  - Sensitive to outliers
  - May not represent central value in skewed data
Median:
- Middle value when data is ordered
- Formula:
  - Odd n: Value at position (n+1)/2
  - Even n: Average of values at n/2 and (n/2)+1
- Example: For [1,3,5,7,9], Median = 5
- Use when:
  - Data has outliers
  - Distribution is skewed
- Limitations:
  - Not influenced by all values
  - Changes less smoothly than mean
Mode:
- Most frequently occurring value
- Formula: Value with highest frequency
- Example: For [1,2,2,3,4], Mode = 2
- Use when:
  - Working with categorical data
  - Need most common value
- Limitations:
  - Can have multiple modes
  - May not exist if all values occur once

Measures of Dispersion

Measures of dispersion describe how spread out data points are from the center. They’re crucial for:

Understanding data variability
Assessing data reliability
Comparing datasets

Common Measures

Variance (σ²)
- Average squared deviation from mean
- Formula: σ² = Σ(x - μ)²/n
- Use when:
  - Detailed spread analysis needed
  - Computing statistical tests
- Limitation: Units are squared
Standard Deviation (σ)
- Square root of variance
- Formula: σ = √(Σ(x - μ)²/n)
- Use when:
  - Need spread in original units
  - Analyzing normal distributions
  - Building ML models

Variance

Variance measures the average squared distance of data points from their mean, indicating data spread and variability.

Key Points

Definition: Average of squared deviations from mean
Population Formula: σ² = Σ(x - μ)²/N
Sample Formula: s² = Σ(x - x̄)²/(n-1)

Why Use n-1 in Sample Variance?

The use of (n-1) instead of n in sample variance is called Bessel’s Correction. Here’s why it matters:

Degrees of Freedom
- When calculating sample variance, we lose one degree of freedom
- This happens because we already used one piece of information (sample mean)
- n-1 accounts for this lost degree of freedom
Bias Correction
- Sample variance with n tends to underestimate population variance
- Using n-1 makes the estimator unbiased
- Formula: s² = Σ(x - x̄)²/(n-1)
Practical Impact
- More noticeable in small samples
- Example:
  - n=5: 20% difference
  - n=100: 1% difference
- Critical for accurate statistical inference

Real-World Example of n-1 in Sample Variance

Imagine a battery manufacturing plant:

Population Data:

All 1000 batteries produced in a day
True population mean (μ) = 1.5V
Population readings vary between 1.3V to 1.7V
True population variance = 0.024V²

Sample Test:

We test only 5 batteries: [1.3V, 1.4V, 1.5V, 1.6V, 1.7V]
Sample mean (x̄) = 1.5V

Variance Calculations:

# Using n (biased)
Variance_n = Σ(x - x̄)²/5
= [(1.3-1.5)² + (1.4-1.5)² + (1.5-1.5)² + (1.6-1.5)² + (1.7-1.5)²]/5
= 0.02V² # Underestimates true variance (0.024V²)

# Using n-1 (unbiased)
Variance_n1 = Σ(x - x̄)²/4
= 0.025V² # Closer to true variance (0.024V²)

Why This Matters:

Using n: 0.02V² (off by 0.004V²)
Using n-1: 0.025V² (off by 0.001V²)
n-1 gives estimate closer to true population variance

This example shows how n-1 provides a better estimate of the true population variance. Note that in real situations, we usually don’t know the true population variance - that’s why we need good estimation methods.

Key Point: Use n-1 for sample variance to get an unbiased estimate of population variance

# Sample of 100 people's weights
mean = 70kg
variance = 25kg²  # Standard deviation ≈ 5kg

# Practical Use
size_range = mean ± (2 × √variance)
# = 70 ± 10kg
# = 60kg to 80kg

# Example with weight data
mean = 70kg
std_dev = 5kg

# Coverage ranges
1σ range = 70 ± 5kg   = 65-75kg   (covers 68%)
2σ range = 70 ± 10kg  = 60-80kg   (covers 95%)  # Most commonly used
3σ range = 70 ± 15kg  = 55-85kg   (covers 99.7%)

Variables

Variables are characteristics that can be measured or categorized. They come in different types:

1. Qualitative (Categorical) Variables

Nominal
- Categories with no order
- Example: Colors (red, blue), Gender (male, female)
- Analysis: Mode, frequency
Ordinal
- Categories with order
- Example: Education (high school, bachelor’s, master’s)
- Analysis: Median, percentiles

2. Quantitative (Numerical) Variables

Discrete
- Countable values
- Example: Number of children, Test score
- Analysis: Mean, standard deviation
Continuous
- Infinite possible values
- Example: Height, Weight, Time
- Analysis: Mean, standard deviation, correlation

Variable Relationships

Independent Variable (X)
- Manipulated/controlled variable
- Example: Study hours
Dependent Variable (Y)
- Outcome variable
- Example: Test score

Note: Variable type determines which statistical methods to use

Random Variables

A random variable is a function that assigns numerical values to outcomes of a random experiment.

Types of Random Variables

Discrete Random Variables
- Takes countable/finite values
- Examples:
  - Number of heads in coin flips
  - Count of defective items
- Properties:
  - Probability Mass Function (PMF)
  - Cumulative Distribution Function (CDF)
Continuous Random Variables
- Takes infinite possible values
- Examples:
  - Height of a person
  - Time to complete a task
- Properties:
  - Probability Density Function (PDF)
  - Cumulative Distribution Function (CDF)

Histogram

A histogram is a graphical representation of the distribution of data. It shows the frequency of each data point in a dataset.

Key Points

Definition: Bar chart showing frequency of data points
Purpose: Visualize data distribution
Components:
- X-axis: Data range (bins)
- Y-axis: Frequency (count or percentage)
- Bars: Represents frequency of data in each bin

Examples

import numpy as np
import matplotlib.pyplot as plt

data = [1, 2, 2, 3, 3, 3, 4, 4, 5]
plt.figure(figsize=(8, 4))
plt.hist(data, bins=5, edgecolor='black')
plt.title('Simple Histogram')
plt.xlabel('Values')
plt.ylabel('Frequency')
plt.show()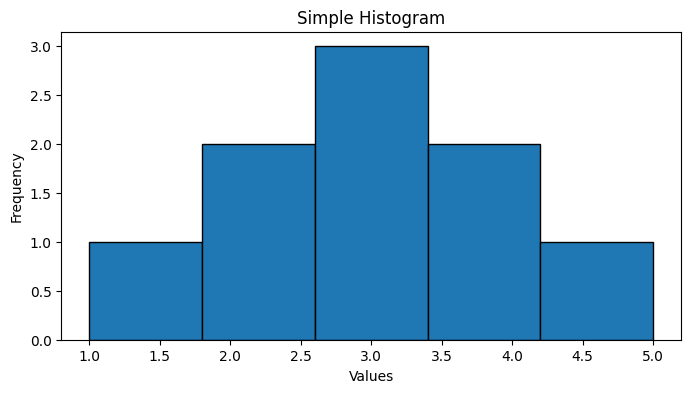

Histogram Output

Percentiles and Quartiles

Percentiles and quartiles are measures that divide a dataset into equal portions.

Percentiles

Divides data into 100 equal parts
Pth percentile: Value below which P% of observations fall
Common uses:
- 50th percentile = median
- Used in standardized testing (e.g., “90th percentile”)

Quartiles

Divides data into 4 equal parts
Q1 (25th percentile): First quartile
Q2 (50th percentile): Median
Q3 (75th percentile): Third quartile
IQR (Interquartile Range) = Q3 - Q1

Example

import numpy as np

data = [2, 4, 6, 8, 10, 12, 14, 16]

# Quartiles
Q1 = np.percentile(data, 25)  # = 5
Q2 = np.percentile(data, 50)  # = 9
Q3 = np.percentile(data, 75)  # = 13
IQR = Q3 - Q1                 # = 8

# Any percentile
p90 = np.percentile(data, 90) # 14.6

5 Number Summary

The 5 number summary is a quick way to describe the distribution of a dataset. It consists of the minimum, first quartile, median, third quartile, and maximum.

Minimum: Smallest value in the dataset
First Quartile (Q1): 25th percentile
Median: 50th percentile
Third Quartile (Q3): 75th percentile
Maximum: Largest value in the dataset

Example

import numpy as np

data = [2, 4, 6, 8, 10, 12, 14, 16]

# 5 Number Summary
summary = np.percentile(data, [0, 25, 50, 75, 100])
print(summary)  # [2.  5.  9.  13. 16.]

Outliers are values that fall outside the range of the 5 number summary.

Lower Outlier: Below (Q1 - 1.5 * IQR)
Upper Outlier: Above (Q3 + 1.5 * IQR)
Interquartile Range (IQR) = Q3 - Q1

Example

import numpy as np

# Sample dataset
data = [1, 2, 2, 3, 4, 10, 20, 25, 30]

# Calculate 5 number summary
min_val = np.min(data)
q1 = np.percentile(data, 25)
median = np.percentile(data, 50)
q3 = np.percentile(data, 75)
max_val = np.max(data)

# Calculate IQR and outlier bounds
iqr = q3 - q1
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr

# Find outliers
outliers = [x for x in data if x < lower_bound or x > upper_bound]

print(f"5 Number Summary:")
print(f"Min: {min_val}")
print(f"Q1: {q1}")
print(f"Median: {median}")
print(f"Q3: {q3}")
print(f"Max: {max_val}")
print(f"Outliers: {outliers}")

Covariance and Correlation

Covariance

Covariance measures how two variables change together. It indicates the direction of the linear relationship between variables.

Formula

Population Covariance: σxy = Σ((x - μx)(y - μy))/N
Sample Covariance: sxy = Σ((x - x̄)(y - ȳ))/(n-1)

Interpretation

Positive covariance: Variables tend to move in same direction
Negative covariance: Variables tend to move in opposite directions
Zero covariance: No linear relationship

Example

import numpy as np

# Height (cm) and Weight (kg) data
height = np.array([170, 175, 160, 180, 165, 172])
weight = np.array([65, 70, 55, 80, 60, 68])

# Calculate means
height_mean = np.mean(height)
weight_mean = np.mean(weight)

# Calculate covariance manually
n = len(height)
covariance = sum((height - height_mean) * (weight - weight_mean)) / (n-1)

# Using NumPy
cov_matrix = np.cov(height, weight)
covariance_np = cov_matrix[0,1]

print(f"Manual Covariance: {covariance:.2f}")
print(f"NumPy Covariance: {covariance_np:.2f}")

# Output:
# Manual Covariance: 58.17
# NumPy Covariance: 58.17

Key Points:

Covariance range: -∞ to +∞
Scale-dependent (affected by units)
Used in:
- Principal Component Analysis
- Portfolio optimization
- Feature selection in ML

Limitations:

Not standardized (hard to compare)
Units are product of both variables

For standardized measurement, use correlation instead.

Correlation

Correlation measures the strength and direction of the linear relationship between two variables. Unlike covariance, it’s standardized between -1 and +1.

Pearson Correlation Coefficient

The most common correlation measure is Pearson’s r:

Formula

Population Correlation: ρxy = Σ((x - μx)(y - μy))/(σxσy)
Sample Correlation: r = Σ((x - x̄)(y - ȳ))/√[Σ(x - x̄)²Σ(y - ȳ)²] = Cov(x,y)/(σxσy)

Interpretation

r = 1: Perfect positive correlation
r = -1: Perfect negative correlation
r = 0: No linear correlation
|r| > 0.7: Strong correlation
0.3 < |r| < 0.7: Moderate correlation
|r| < 0.3: Weak correlation

Example

import numpy as np
import matplotlib.pyplot as plt

# Sample data
x = np.array([1, 2, 3, 4, 5])
y1 = np.array([2, 4, 6, 8, 10])  # Perfect positive
y2 = np.array([10, 8, 6, 4, 2])  # Perfect negative
y3 = np.array([2, 5, 4, 5, 3])   # Weak correlation

def plot_correlation(x, y, title):
    plt.scatter(x, y)
    plt.title(f'{title} (r = {np.corrcoef(x,y)[0,1]:.2f})')
    plt.xlabel('X')
    plt.ylabel('Y')

# Create subplots
plt.figure(figsize=(15, 5))

plt.subplot(131)
plot_correlation(x, y1, "Perfect Positive")

plt.subplot(132)
plot_correlation(x, y2, "Perfect Negative")

plt.subplot(133)
plot_correlation(x, y3, "Weak")

plt.tight_layout()
plt.show()

# Calculate correlations
print(f"Positive correlation: {np.corrcoef(x,y1)[0,1]:.2f}") # 1.00
print(f"Negative correlation: {np.corrcoef(x,y2)[0,1]:.2f}") # -1.00
print(f"Weak correlation: {np.corrcoef(x,y3)[0,1]:.2f}") # 0.24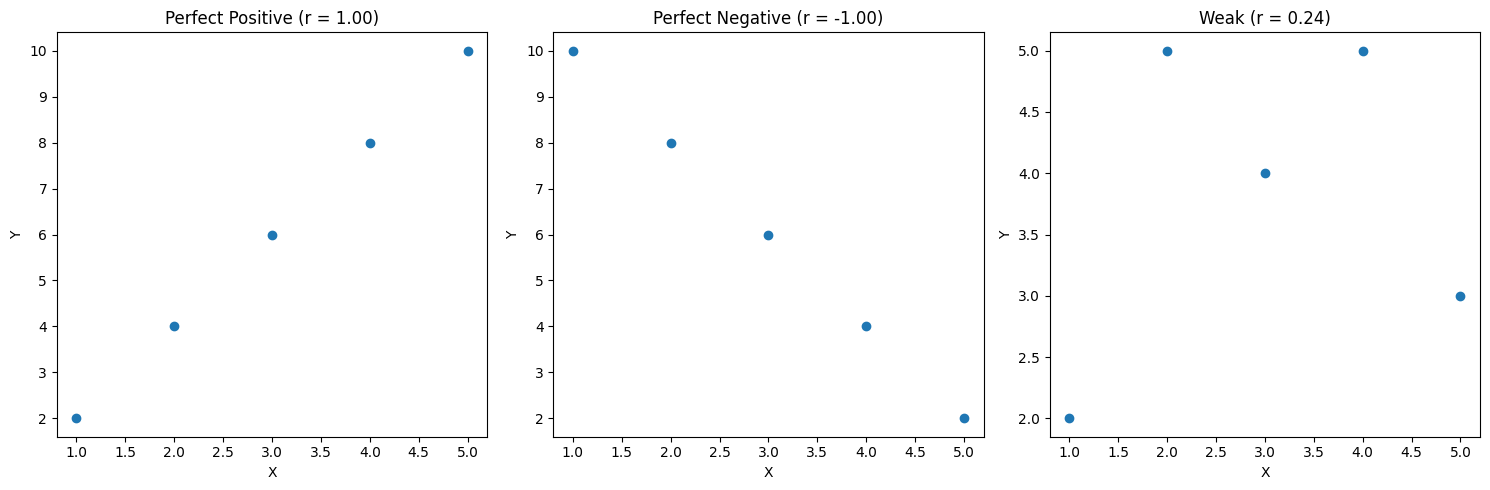

Correlation

Key Properties

Scale-independent (standardized)
Always between -1 and +1
No units
Symmetric: corr(x,y) = corr(y,x)

Common Uses

Feature selection in ML
Financial portfolio analysis
Scientific research
Quality control

Limitations

Only measures linear relationships
Sensitive to outliers
Correlation ≠ causation
Requires numeric data

Real-World Example

import pandas as pd

# Student data
data = {
    'study_hours': [2, 3, 3, 4, 4, 5, 5, 6],
    'test_score': [65, 70, 75, 80, 85, 85, 90, 95]
}

df = pd.DataFrame(data)

# Calculate correlation
correlation = df['study_hours'].corr(df['test_score'])

print(f"Correlation between study hours and test scores: {correlation:.2f}")
# Output: Correlation between study hours and test scores: 0.97

Important Notes

High correlation doesn’t imply causation
Always visualize data - don’t rely solely on correlation coefficient
Consider non-linear relationships
Check for outliers that might affect correlation

Spearman Correlation

Spearman correlation measures monotonic relationships between variables (whether they move in the same direction, regardless of the rate of change).

Formula

First convert values to ranks
- rank(x): Rank values of first variable
- rank(y): Rank values of second variable
Calculate differences d = rank(x) - rank(y)
Square the differences d² = (rank(x) - rank(y))²
Sum all squared differences Σd² = sum of all d²
Final formula: ρ = 1 - (6 * Σd²)/(n(n² - 1))

Example with numbers: x = [1,2,3] y = [2,1,3]

ranks_x = [1,2,3] ranks_y = [2,1,3]

d = [1-2, 2-1, 3-3] = [-1,1,0] d² = [1,1,0] Σd² = 2 n = 3

ρ = 1 - (6 * 2)/(3(9-1)) = 1 - 12/24 = 0.5

Example

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Online Store Example
# X: Product Price
# Y: Number of Sales
price = np.array([10, 20, 30, 40, 50, 60, 70, 80, 90, 100])
sales = np.array([100, 90, 80, 65, 45, 30, 20, 15, 12, 10])

# Calculate Correlations
pearson = stats.pearsonr(price, sales)[0]
spearman = stats.spearmanr(price, sales)[0]

# Plotting
plt.figure(figsize=(10, 6))
plt.scatter(price, sales)
plt.title('Price vs Sales: Non-linear Relationship')
plt.xlabel('Price ($)')
plt.ylabel('Number of Sales')

# Add correlation values
plt.text(20, 30, f'Pearson r: {pearson:.2f}')
plt.text(20, 20, f'Spearman r: {spearman:.2f}')
plt.grid(True)
plt.show()

print(f"Pearson Correlation: {pearson:.2f}")   # -0.89
print(f"Spearman Correlation: {spearman:.2f}") # -1.00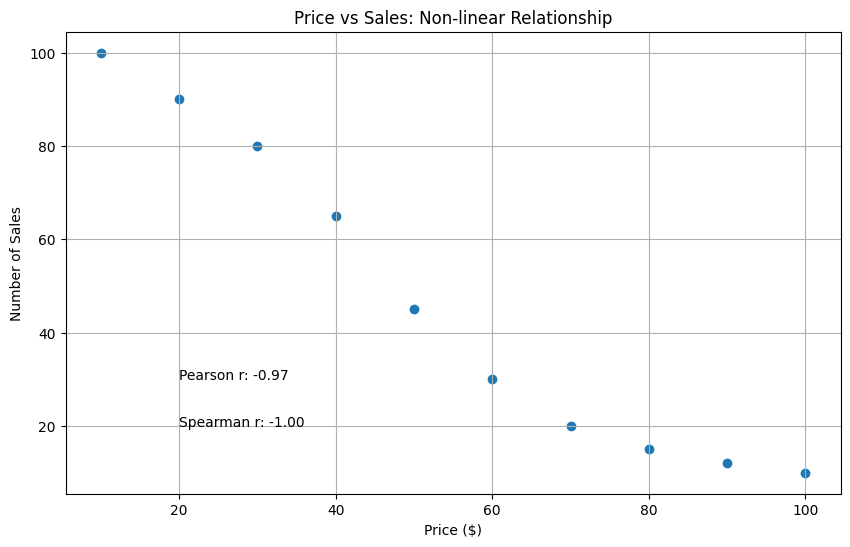

Spearman Correlation

Probability

Probability is a measure of the likelihood of an event occurring. It’s a fundamental concept in statistics and data science.

Additive Rule

Mutually Exclusive Events

Events that cannot occur at the same time.

Formula: P(A or B) = P(A) + P(B)

Example:

Rolling a die:
- P(getting 1 or 2) = P(1) + P(2) = 1/6 + 1/6 = 1/3
- Events are mutually exclusive since you can’t roll 1 and 2 simultaneously

Non-Mutually Exclusive Events

Events that can occur at the same time.

Formula: P(A or B) = P(A) + P(B) - P(A and B)

Example:

Drawing a card:
- P(getting King or Heart) = P(King) + P(Heart) - P(King of Heart)
- = 4/52 + 13/52 - 1/52 = 16/52
- Events overlap since King of Hearts is possible

Multiplicative Rule

The multiplicative rule calculates probability of multiple events occurring together.

Independent Events

Events where occurrence of one doesn’t affect the other.

Formula: P(A and B) = P(A) × P(B)

Example:

Flipping a coin twice:
- P(2 heads) = P(head1) × P(head2) = 1/2 × 1/2 = 1/4

Dependent Events

Events where occurrence of one affects the other.

Formula: P(A and B) = P(A) × P(B|A)

Example:

Drawing 2 cards without replacement:
- P(2 aces) = P(ace1) × P(ace2|ace1)
- = 4/52 × 3/51 = 1/221

Relationship between PMF, PDF, and CDF

1. PMF (Probability Mass Function)

A PMF describes the probability distribution of a discrete random variable.

Definition

Maps each value of discrete random variable to its probability
P(X = x) gives probability of X taking value x
Sum of all probabilities must equal 1

Properties

0 ≤ P(X = x) ≤ 1
∑P(X = x) = 1
Only for discrete variables

Real-World Example: Dice Roll Game

import numpy as np
import matplotlib.pyplot as plt

# Fair die PMF
outcomes = np.array([1, 2, 3, 4, 5, 6])
probabilities = np.array([1/6] * 6)

# Loaded die PMF (favors 6)
loaded_prob = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])

# Plot
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.bar(outcomes, probabilities)
plt.title('Fair Die PMF')
plt.xlabel('Outcome')
plt.ylabel('Probability')

plt.subplot(1, 2, 2)
plt.bar(outcomes, loaded_prob)
plt.title('Loaded Die PMF')
plt.xlabel('Outcome')
plt.show()

# Calculate probability of rolling even numbers
fair_even = sum(probabilities[1::2])    # 0.5
loaded_even = sum(loaded_prob[1::2])    # 0.7

print(f"P(Even) Fair Die: {fair_even}") # 0.5
print(f"P(Even) Loaded Die: {loaded_even}") # 0.7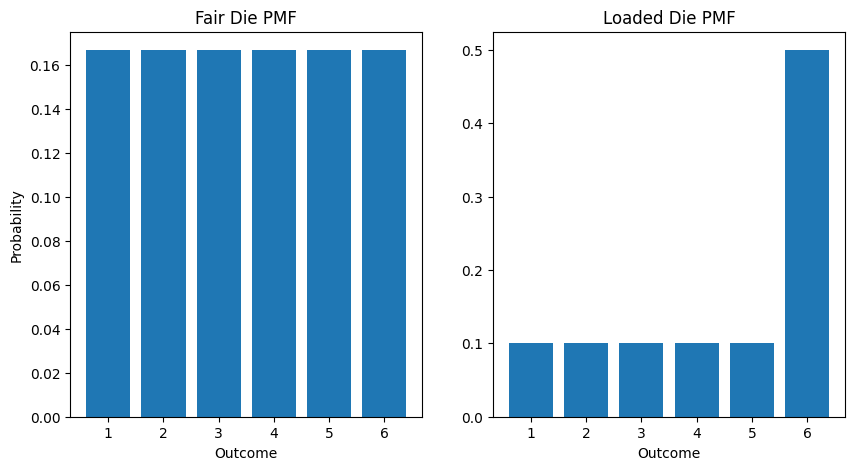

PMF

PMF helps in making probability-based decisions in discrete scenarios like manufacturing defects, customer counts, or game outcomes.

CDF (Cumulative Distribution Function) For Discrete Variables

CDF gives the probability that a random variable X is less than or equal to a value x.

Formula

F(x) = P(X ≤ x) = ∑ P(X = t) for all t ≤ x

Example: Die Roll

import numpy as np
import matplotlib.pyplot as plt

# Define probabilities
outcomes = np.arange(1, 7)  # [1,2,3,4,5,6]
fair_prob = np.ones(6) / 6  # [1/6, 1/6, 1/6, 1/6, 1/6, 1/6]
loaded_prob = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])

# Calculate CDFs
fair_cdf = np.cumsum(fair_prob)
loaded_cdf = np.cumsum(loaded_prob)

# Create plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))

# Plot fair die CDF
ax1.step(outcomes, fair_cdf, where='post')
ax1.set(title='Fair Die CDF', xlabel='Outcome', ylabel='Cumulative Probability')
ax1.grid(True)

# Plot loaded die CDF
ax2.step(outcomes, loaded_cdf, where='post')
ax2.set(title='Loaded Die CDF', xlabel='Outcome')
ax2.grid(True)

plt.tight_layout()
plt.show()

# Print probabilities for X ≤ 4
print(f"P(X ≤ 4) Fair Die: {fair_cdf[3]:.3f}") # 0.667
print(f"P(X ≤ 4) Loaded Die: {loaded_cdf[3]:.3f}") # 0.400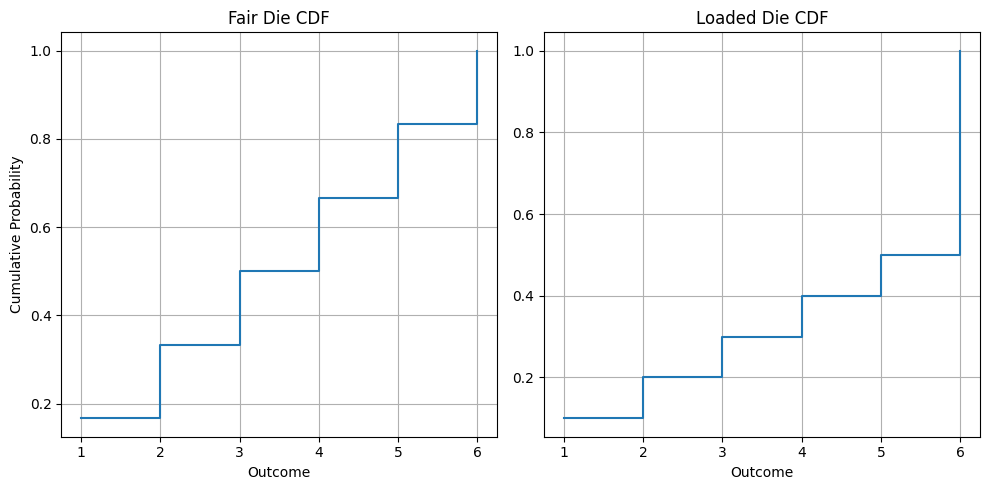

Discrete CDF

2. PDF (Probability Density Function)

A PDF describes the probability distribution of a continuous random variable.

Why PDF for Continuous Random Variables?

Impossible to List All Values
- Continuous variables have infinite possible values
- Can’t assign individual probabilities like PMF
Zero Individual Probability
- P(X = x) = 0 for any exact value
- Example: P(height = exactly 170.000000…cm) = 0
Range Probabilities
- PDF helps calculate probability over intervals
- P(a ≤ X ≤ b) = ∫[a to b] f(x)dx
- Example: P(170 ≤ height ≤ 175)

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Height Distribution in Adult Population
mean_height = 170  # cm
std_dev = 10       # cm

# Create height range
heights = np.linspace(140, 200, 100)

# Calculate PDF using normal distribution
pdf = norm.pdf(heights, mean_height, std_dev)

# Plot
plt.figure(figsize=(10, 6))
plt.plot(heights, pdf)
plt.title('Height Distribution in Adult Population')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')

# Calculate probabilities
# Probability of height between 160-180cm
prob_160_180 = norm.cdf(180, mean_height, std_dev) - norm.cdf(160, mean_height, std_dev)
print(f"Probability of height between 160-180cm: {prob_160_180:.2%}")  # ≈ 68%

# Probability of height above 190cm
prob_above_190 = 1 - norm.cdf(190, mean_height, std_dev)
print(f"Probability of height above 190cm: {prob_above_190:.2%}")      # ≈ 2.3%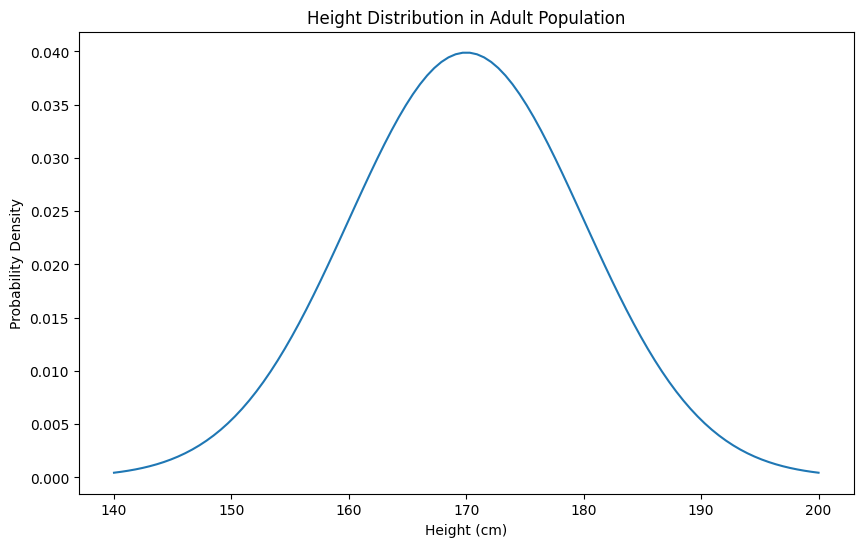

Continuous PDF

Density

Density in statistics refers to how tightly packed data points or probability is in a given interval or region.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

mean = 170
std = 10

# Single point density doesn't tell much
point_density = norm.pdf(170, mean, std)
print(f"Density at 170cm: {point_density:.4f}")  # 0.0399
# This number 0.0399 alone is meaningless without context

# What makes sense is comparing densities
heights = [150, 160, 170, 180, 190]
densities = [norm.pdf(h, mean, std) for h in heights]

plt.figure(figsize=(10, 6))
x = np.linspace(140, 200, 1000)
y = norm.pdf(x, mean, std)

plt.plot(x, y)

# Plot points for comparison
for h, d in zip(heights, densities):
    plt.plot(h, d, 'o', label=f'Height={h}cm\nDensity={d:.4f}')

plt.title('Height Distribution - Comparing Densities')
plt.xlabel('Height (cm)')
plt.ylabel('Density')
plt.legend()
plt.grid(True)

# Now we can see:
# - 170cm has highest density (most common)
# - 150cm and 190cm have low density (less common)
# - Comparison gives meaning to the numbers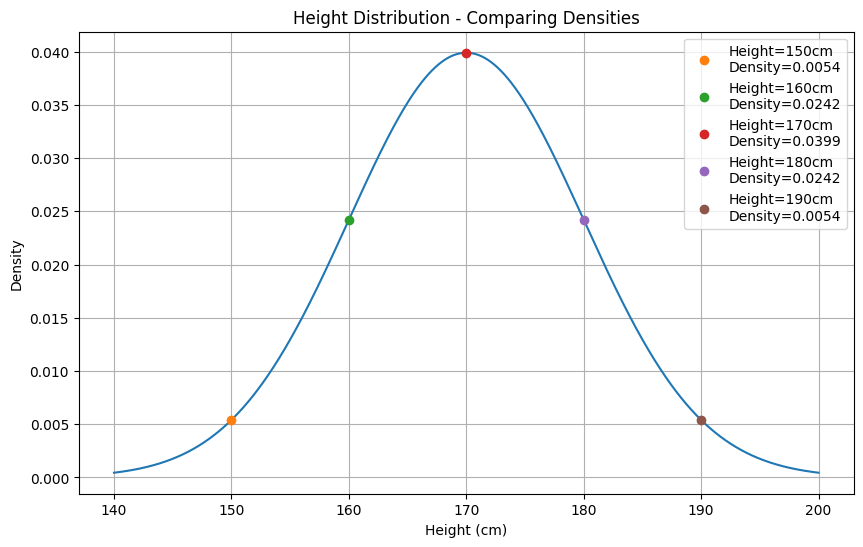

Density

CDF (Cumulative Distribution Function) For Continuous Variables

The Cumulative Distribution Function (CDF) for a continuous random variable X, denoted as F(x), represents the probability that X takes on a value less than or equal to x.

Mathematical Definition

F(x) = P(X ≤ x) = ∫[from -∞ to x] f(t)dt

where f(t) is the probability density function (PDF)

Key Properties

Bounds
- 0 ≤ F(x) ≤ 1 for all x
- lim[x→-∞] F(x) = 0
- lim[x→∞] F(x) = 1
Continuity
- Right-continuous
- Monotonically increasing (never decreases)
Probability Calculations
- P(a < X ≤ b) = F(b) - F(a)
- P(X > a) = 1 - F(a)
Relationship to PDF
- F’(x) = f(x) (derivative of CDF is PDF)
- F(x) is the integral of f(x)

Simple Example: Height Distribution in a Class

Consider heights of students in a class of 100:

Scenario:

Heights range from 150cm to 190cm
CDF tells us probability of height being less than or equal to a value

Simple Interpretations:

F(160) = 0.2 means 20% of students are 160cm or shorter
F(170) = 0.5 means 50% of students are 170cm or shorter
F(180) = 0.9 means 90% of students are 180cm or shorter

Practical Uses:

Finding median height: Where F(x) = 0.5
Ordering uniforms: What size covers 80% of students
Identifying unusually tall/short: Heights where F(x) < 0.1 or F(x) > 0.9

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Parameters
mean_height = 170  # mean height in cm
std_dev = 10      # standard deviation in cm
n_students = 100

# Generate student heights
np.random.seed(42)  # for reproducibility
heights = np.random.normal(mean_height, std_dev, n_students)

# Calculate empirical CDF
heights_sorted = np.sort(heights)
cumulative_prob = np.arange(1, len(heights) + 1) / len(heights)

# Plot
plt.figure(figsize=(10, 6))

# Empirical CDF
plt.plot(heights_sorted, cumulative_prob, 'b-', label='Empirical CDF')

# Add reference lines
plt.axhline(y=0.2, color='r', linestyle='--', alpha=0.5)
plt.axhline(y=0.5, color='r', linestyle='--', alpha=0.5)
plt.axhline(y=0.9, color='r', linestyle='--', alpha=0.5)

# Labels and title
plt.title('Height Distribution CDF in Class')
plt.xlabel('Height (cm)')
plt.ylabel('Cumulative Probability')
plt.grid(True)

# Find specific values
height_20 = np.percentile(heights, 20)
height_50 = np.percentile(heights, 50)
height_90 = np.percentile(heights, 90)

print(f"20th percentile (F(x) = 0.2): {height_20:.1f}cm") # 162.6cm
print(f"50th percentile (F(x) = 0.5): {height_50:.1f}cm") # 168.7cm
print(f"90th percentile (F(x) = 0.9): {height_90:.1f}cm") # 180.1cm

plt.show()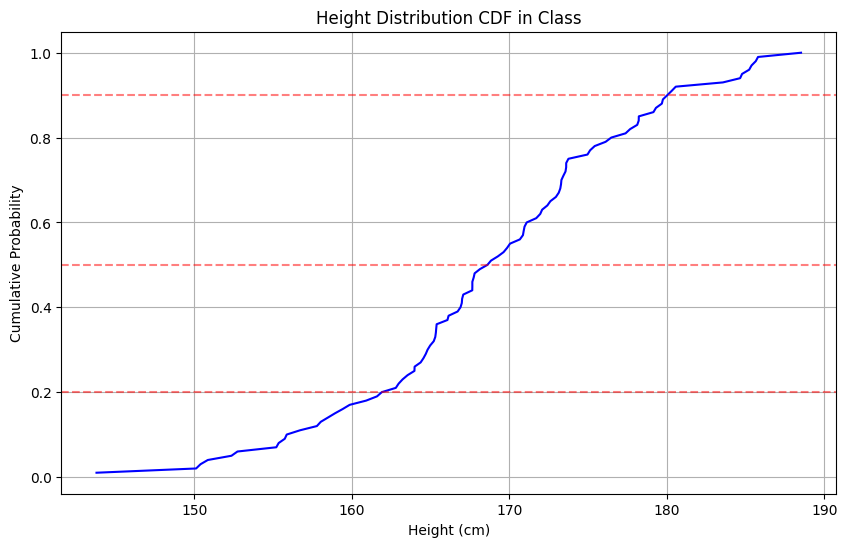

Continuous CDF

Types of Probability Distributions

Bernoulli Distribution

The Bernoulli distribution models binary outcomes - experiments with exactly two possible results (success/failure).

Properties

Parameter: p (probability of success)
Possible Values: x ∈ 1
- x = 1 (success): probability = p
- x = 0 (failure): probability = 1-p
PMF: P(X = x) = p^x * (1-p)^(1-x)
Mean: E(X) = p
Variance: Var(X) = p(1-p)

Common Applications

Coin flips (heads/tails)
Quality control (defective/non-defective)
Email (spam/not spam)
Medical tests (positive/negative)

Example Implementation

import numpy as np
import matplotlib.pyplot as plt

class BernoulliTrial:
    def __init__(self, p):
        self.p = p

    def pmf(self, x):
        return self.p if x == 1 else (1-self.p)

    def simulate(self, n_trials):
        return np.random.binomial(n=1, p=self.p, size=n_trials)

# Example: Biased coin (p=0.7)
b = BernoulliTrial(p=0.7)
trials = b.simulate(1000)

# Results
success_rate = np.mean(trials)
print(f"Theoretical probability: 0.7")
print(f"Observed probability: {success_rate:.3f}")

# Visualize
plt.figure(figsize=(8, 4))
plt.bar(['Failure (0)', 'Success (1)'],
        [1-success_rate, success_rate])
plt.title('Bernoulli Distribution (p=0.7)')
plt.ylabel('Probability')
plt.ylim(0, 1)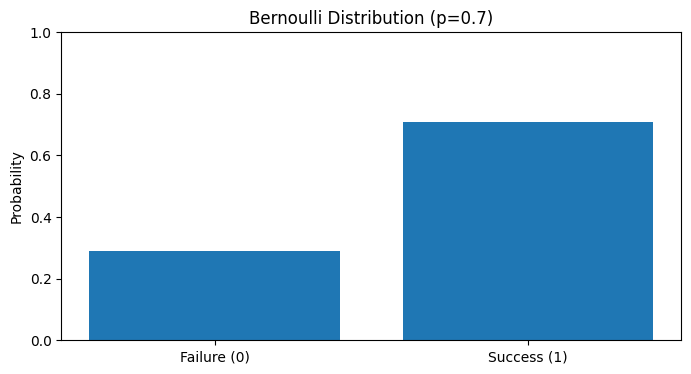

Bernoulli Distribution

Real-World Example: Email Spam Detection

# Simple spam detector
class SpamDetector:
    def __init__(self, spam_probability=0.3):
        self.b = BernoulliTrial(spam_probability)

    def classify_email(self):
        return "Spam" if self.b.simulate(1)[0] else "Not Spam"

# Simulate email classification
detector = SpamDetector()
n_emails = 100
classifications = [detector.classify_email() for _ in range(n_emails)]

spam_ratio = classifications.count("Spam") / n_emails
print(f"Classified {spam_ratio:.1%} emails as spam")
// Classified 26.0% emails as spam

Key Points

Independence: Each trial is independent
Memory-less: Previous outcomes don’t affect next trial
Fixed probability: p remains constant across trials

Relationship to Other Distributions

Foundation for Binomial distribution (n Bernoulli trials)
Special case of Binomial where n=1
Building block for more complex probability models

Binomial Distribution

The Binomial distribution models the number of successes in n independent Bernoulli trials.

Properties

Parameters:
- n (number of trials)
- p (probability of success)
PMF: P(X = k) = C(n,k) * p^k * (1-p)^(n-k)
Mean: E(X) = np
Variance: Var(X) = np(1-p)

Example Implementation

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

class BinomialDistribution:
    def __init__(self, n, p):
        self.n = n
        self.p = p

    def pmf(self, k):
        return binom.pmf(k, self.n, self.p)

    def simulate(self, n_trials):
        return np.random.binomial(self.n, self.p, n_trials)

# Example: Rolling a fair die 10 times, counting 6s
n, p = 10, 1/6  # 10 rolls, P(6) = 1/6
b = BinomialDistribution(n, p)

# Calculate PMF for all possible values
k = np.arange(0, n+1)
probabilities = [b.pmf(ki) for ki in k]

# Plot
plt.figure(figsize=(10, 5))
plt.bar(k, probabilities)
plt.title(f'Binomial Distribution (n={n}, p={p:.2f})')
plt.xlabel('Number of Successes (k)')
plt.ylabel('Probability')
plt.grid(True, alpha=0.3)

# Expected value and variance
mean = n * p
var = n * p * (1-p)
print(f"Expected number of 6s: {mean:.2f}") # 1.67
print(f"Variance: {var:.2f}") # 1.39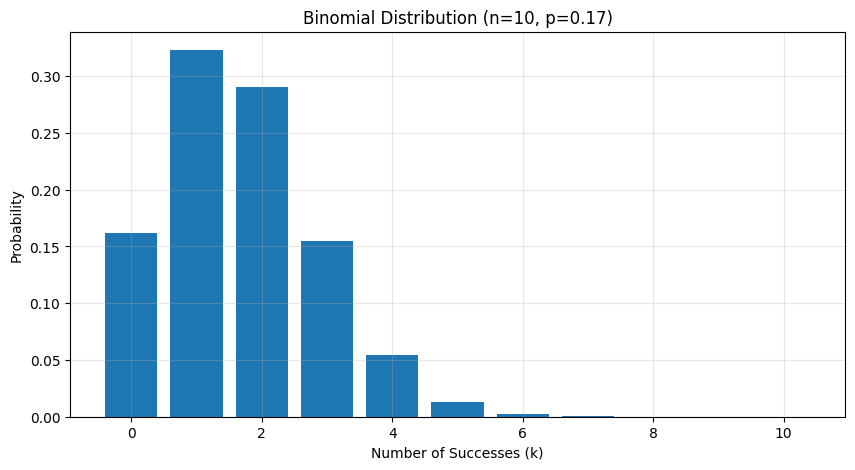

Binomial Distribution

Real-World Example: Quality Control

# Manufacturing defect inspection
class QualityControl:
    def __init__(self, batch_size=20, defect_rate=0.05):
        self.binom = BinomialDistribution(batch_size, defect_rate)

    def inspect_batch(self):
        return self.binom.simulate(1)[0]

    def is_batch_acceptable(self, max_defects=2):
        defects = self.inspect_batch()
        return {
            'defects': defects,
            'acceptable': defects <= max_defects
        }

# Simulate batch inspections
qc = QualityControl()
n_batches = 1000
inspections = [qc.is_batch_acceptable() for _ in range(n_batches)]

acceptance_rate = sum(i['acceptable'] for i in inspections) / n_batches
print(f"Batch acceptance rate: {acceptance_rate:.1%}")
// Batch acceptance rate: 92.7%

Common Applications

Quality control in manufacturing
A/B testing success counts
Survey response modeling
Genetic inheritance patterns

Key Points

Sum of independent Bernoulli trials
Requires fixed probability p
Trials must be independent
Only whole numbers (discrete)

Poisson Distribution

The Poisson distribution models the number of events occurring in a fixed interval when these events happen at a constant average rate and independently of each other.

Properties

Parameter: λ (lambda) - average number of events per interval
PMF: P(X = k) = (λ^k * e^-λ) / k!
Mean: E(X) = λ
Variance: Var(X) = λ

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

class PoissonDistribution:
    def __init__(self, lambda_param):
        self.lambda_param = lambda_param

    def pmf(self, k):
        return poisson.pmf(k, self.lambda_param)

    def simulate(self, n_samples):
        return np.random.poisson(self.lambda_param, n_samples)

# Example: Website visits per hour (average 5 visits)
lambda_param = 5
p = PoissonDistribution(lambda_param)

# Calculate PMF for values 0 to 12
k = np.arange(0, 13)
probabilities = [p.pmf(ki) for ki in k]

# Visualization
plt.figure(figsize=(10, 6))
plt.bar(k, probabilities)
plt.title(f'Poisson Distribution (λ={lambda_param})')
plt.xlabel('Number of Events (k)')
plt.ylabel('Probability')
plt.grid(True, alpha=0.3)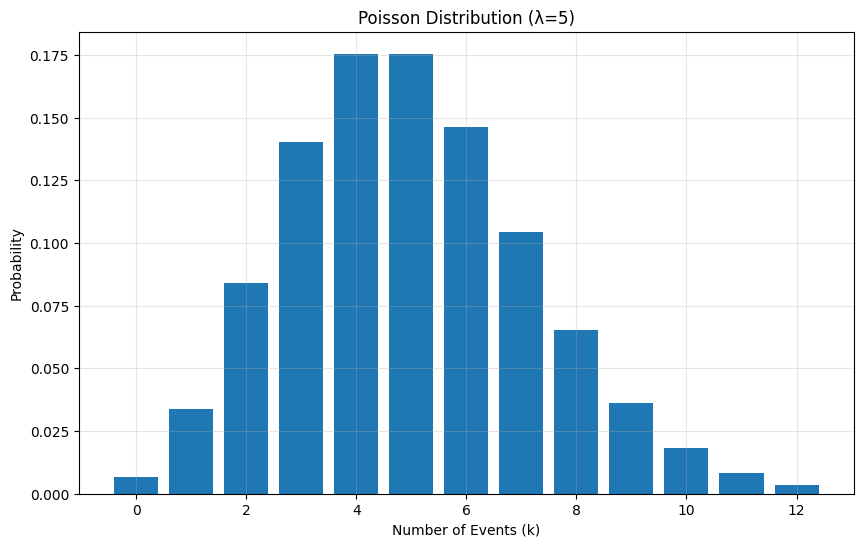

Poisson Distribution

Common Applications

Customer Service
- Number of customers arriving per hour
- Support tickets received per day
- Phone calls to call center
Web Traffic
- Page views per minute
- Server requests per second
- Error occurrences per day
Quality Control
- Defects per unit area
- Flaws per length of material
- Errors per page
Natural Phenomena
- Radioactive decay events
- Mutations in DNA sequence
- Natural disasters per year

Real-World Example: Server Monitoring

class ServerMonitor:
    def __init__(self, avg_requests_per_minute=30):
        self.poisson = PoissonDistribution(avg_requests_per_minute)

    def simulate_minute(self):
        return self.poisson.simulate(1)[0]

    def check_load(self, threshold=50):
        requests = self.simulate_minute()
        return {
            'requests': requests,
            'overloaded': requests > threshold,
            'utilization': requests / threshold
        }

# Monitor server for an hour
monitor = ServerMonitor()
hour_data = [monitor.check_load() for _ in range(60)]

# Analysis
overloaded_minutes = sum(minute['overloaded'] for minute in hour_data)
avg_utilization = np.mean([minute['utilization'] for minute in hour_data])

print(f"Minutes overloaded: {overloaded_minutes}") // Minutes overloaded: 0
print(f"Average utilization: {avg_utilization:.1%}") // Average utilization: 56.5%

Key Characteristics

Independence
- Events occur independently
- Past events don’t influence future events
Rate Consistency
- Average rate (λ) remains constant
- No systematic variation in event frequency
Rare Events
- Individual events are rare relative to opportunities
- Many opportunities for events to occur
No Upper Limit
- Can theoretically take any non-negative integer value
- Practical limits depend on λ

Relationship to Other Distributions

Binomial Distribution
- Poisson is limit of binomial as n��∞, p→0, np=λ
- Used when events are rare but opportunities numerous
Exponential Distribution
- Time between Poisson events follows exponential distribution
- If events are Poisson(λ), waiting times are Exp(1/λ)

Assumptions and Limitations

Rate Stability
- Assumes constant average rate
- May not fit if rate varies significantly
Independence
- Events must be independent
- Not suitable for contagious or clustered events
No Simultaneous Events
- Events occur one at a time
- May need modifications for concurrent events
Memory-less Property
- Future events independent of past
- May not suit events with temporal dependencies

# Example: Testing Poisson assumptions
def test_rate_stability(data, window_size=10):
    """Test if event rate is stable over time"""
    windows = np.array_split(data, len(data)//window_size)
    means = [np.mean(w) for w in windows]
    return np.std(means) / np.mean(means)  # CV should be small

# Generate sample data
p = PoissonDistribution(lambda_param=5)
data = p.simulate(1000)

stability_metric = test_rate_stability(data)
print(f"Rate stability metric: {stability_metric:.3f}")
# Lower values indicate more stable rate
// Rate stability metric: 0.138

Normal Distribution/Gaussian Distribution

The Normal (or Gaussian) distribution is a continuous probability distribution that is symmetric around its mean, showing a characteristic “bell-shaped” curve.

Properties

Parameters:
- μ (mean): Center of distribution
- σ (standard deviation): Spread of distribution
PDF: f(x) = (1/(σ√(2π))) * e^(-(x-μ)²/(2σ²))
Mean = Median = Mode: All equal to μ
68-95-99.7 Rule:
- 68% of data within μ ± 1σ
- 95% of data within μ ± 2σ
- 99.7% of data within μ ± 3σ

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

class NormalDistribution:
    def __init__(self, mu=0, sigma=1):
        self.mu = mu
        self.sigma = sigma

    def pdf(self, x):
        return norm.pdf(x, self.mu, self.sigma)

    def simulate(self, n_samples):
        return np.random.normal(self.mu, self.sigma, n_samples)

# Example: Height Distribution
mu, sigma = 170, 10  # mean=170cm, std=10cm
normal = NormalDistribution(mu, sigma)

# Generate x values and corresponding probabilities
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 100)
y = normal.pdf(x)

# Plot
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'b-', label='PDF')

# Add standard deviation ranges
for i, pct in [(1, 0.68), (2, 0.95), (3, 0.997)]:
    plt.fill_between(x, y,
                     where=(x >= mu-i*sigma) & (x <= mu+i*sigma),
                     alpha=0.2,
                     label=f'±{i}σ ({pct:.1%})')

plt.title('Normal Distribution of Heights')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)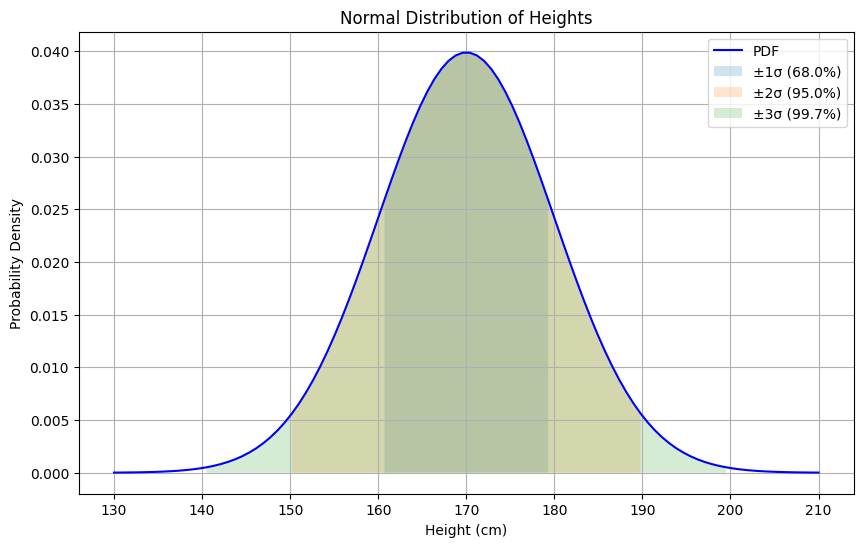

Normal Distribution

Common Applications

Physical Measurements
- Height, weight
- Manufacturing dimensions
- Measurement errors
Natural Phenomena
- IQ scores
- Blood pressure
- Test scores
Financial Markets
- Stock returns
- Price fluctuations
- Risk modeling

Real-World Example: Quality Control

class ProductionLine:
    def __init__(self, target_length=100, tolerance=0.5):
        self.normal = NormalDistribution(target_length, tolerance/3)
        self.tolerance = tolerance

    def produce_item(self):
        length = self.normal.simulate(1)[0]
        return {
            'length': length,
            'in_spec': abs(length - self.normal.mu) <= self.tolerance
        }

    def analyze_batch(self, size=1000):
        batch = [self.produce_item() for _ in range(size)]
        defect_rate = 1 - sum(item['in_spec'] for item in batch) / size
        return f"Defect rate: {defect_rate:.2%}"

# Simulate production
line = ProductionLine()
print(line.analyze_batch())  # Expected ≈ 0.20% defect rate

Z-Score (Standard Score)

Z-score measures how many standard deviations away from the mean a data point is:

Formula: z = (x - μ) / σ
Standardizes any normal distribution to N(0,1)
Useful for comparing values from different distributions

def calculate_z_score(x, mu, sigma):
    return (x - mu) / sigma

# Example
height = 185  # cm
z = calculate_z_score(height, mu=170, sigma=10)
print(f"Z-score for {height}cm: {z:.2f}")  # 1.50
print(f"Percentile: {norm.cdf(z):.2%}")    # 93.32%

Central Limit Theorem (CLT)

The CLT states that the sampling distribution of the mean approaches a normal distribution as sample size increases, regardless of the underlying distribution:

def demonstrate_clt(distribution, sample_size, n_samples):
    means = [np.mean(distribution(sample_size))
             for _ in range(n_samples)]
    return means

# Example with uniform distribution
uniform_samples = lambda n: np.random.uniform(0, 1, n)
sample_means = demonstrate_clt(uniform_samples, 30, 1000)

plt.figure(figsize=(10, 6))
plt.hist(sample_means, bins=30, density=True)
plt.title('Sampling Distribution of Mean (n=30)')
plt.xlabel('Sample Mean')
plt.ylabel('Density')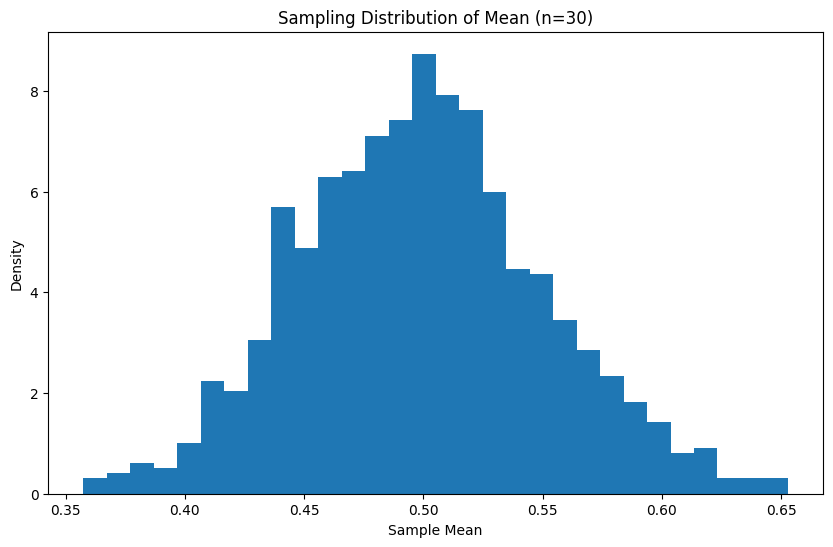

Central Limit Theorem

Key Points

Symmetry
- Perfectly symmetric around mean
- Skewness = 0
- Kurtosis = 3
Standardization
- Any normal distribution can be standardized
- Z-scores allow comparison across distributions
Empirical Rule
- 68-95-99.7 rule for data distribution
- Useful for quick probability estimates
Properties
- Sum of normal variables is normal
- Linear combination of normal variables is normal
- Independent of sample size (unlike t-distribution)

Standard Normal Distribution

The Standard Normal Distribution is a special case of the normal distribution where μ = 0 and σ = 1. It’s often denoted as N(0,1) and serves as a reference distribution.

Properties

Mean (μ) = 0
Standard Deviation (σ) = 1
PDF: f(z) = (1/√(2π)) * e^(-z²/2)
Symmetric around zero
Total area = 1

Z-Table Areas

z = ±1: 68% of data
z = ±2: 95% of data
z = ±3: 99.7% of data

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

def plot_standard_normal():
    z = np.linspace(-4, 4, 100)
    pdf = norm.pdf(z, 0, 1)

    plt.figure(figsize=(10, 6))
    plt.plot(z, pdf, 'b-', label='PDF')

    # Shade regions
    colors = ['red', 'blue', 'green']
    alphas = [0.1, 0.1, 0.1]
    for i, (c, a) in enumerate(zip(colors, alphas), 1):
        mask = (z >= -i) & (z <= i)
        plt.fill_between(z[mask], pdf[mask], color=c, alpha=a,
                        label=f'±{i}σ ({norm.cdf(i)-norm.cdf(-i):.1%})')

    plt.title('Standard Normal Distribution')
    plt.xlabel('Z-Score')
    plt.ylabel('Probability Density')
    plt.grid(True)
    plt.legend()
    return plt

# Example usage
plot = plot_standard_normal()
plt.show()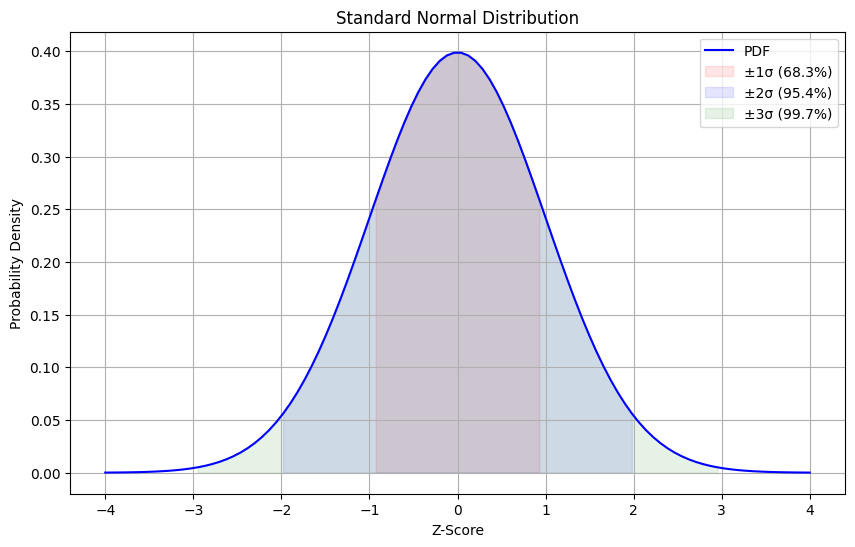

Standard Normal Distribution

Common Z-Score Values

# Key probability points
z_scores = {
    0.90: 1.28,  # 90% confidence
    0.95: 1.96,  # 95% confidence
    0.99: 2.58   # 99% confidence
}

# Example: Finding probabilities
def get_z_probability(z):
    return norm.cdf(z) - norm.cdf(-z)

print(f"P(-1 < Z < 1): {get_z_probability(1):.4f}")  # 0.6827
print(f"P(-2 < Z < 2): {get_z_probability(2):.4f}")  # 0.9545
print(f"P(-3 < Z < 3): {get_z_probability(3):.4f}")  # 0.9973

Applications

Standardization

def standardize(x, mu, sigma):
    return (x - mu) / sigma

Example: Test scores

scores = [75, 82, 90, 68, 95] mu = np.mean(scores) sigma = np.std(scores) z_scores = [standardize(x, mu, sigma) for x in scores]

2. **Hypothesis Testing**
   ```python
   def z_test(sample_mean, pop_mean, pop_std, n):
       z = (sample_mean - pop_mean) / (pop_std / np.sqrt(n))
       p_value = 2 * (1 - norm.cdf(abs(z)))  # Two-tailed
       return z, p_value

Confidence Intervals

def confidence_interval(mean, std, n, confidence=0.95):
    z = norm.ppf((1 + confidence) / 2)
    margin = z * (std / np.sqrt(n))
    return mean - margin, mean + margin

Key Uses

Reference for normalizing data
Base for statistical inference
Quality control limits
Risk assessment
Hypothesis testing

Transformation

To convert between normal distributions:

From N(μ,σ) to N(0,1): Z = (X - μ) / σ
From N(0,1) to N(μ,σ): X = Zσ + μ

# Example: Converting between distributions
def transform_distribution(x, from_params, to_params):
    """
    Transform value between normal distributions
    from_params: tuple of (mean, std) of original distribution
    to_params: tuple of (mean, std) of target distribution
    """
    from_mean, from_std = from_params
    to_mean, to_std = to_params

    # First standardize
    z = (x - from_mean) / from_std
    # Then transform to new distribution
    return z * to_std + to_mean

# Example usage
x = 85  # Score from N(75, 10)
new_x = transform_distribution(x, (75, 10), (100, 15))
print(f"Score of {x} transforms to {new_x:.1f}")
// Score of 85 transforms to 115.0

Uniform Distribution

The Uniform Distribution is a probability distribution where all outcomes in a given interval are equally likely to occur. It comes in two forms: discrete and continuous.

Types of Uniform Distributions

Continuous Uniform Distribution
- Defined over continuous interval [a,b]
- Also called “rectangular distribution”
- Every point in interval has equal probability density
Discrete Uniform Distribution
- Defined over finite set of equally spaced values
- Each value has equal probability
- Example: Fair die (values 1-6)

Mathematical Properties

Continuous Uniform
- PDF: f(x) = 1/(b-a) for a ≤ x ≤ b, 0 otherwise
- CDF: F(x) = (x-a)/(b-a) for a ≤ x ≤ b
- Mean: μ = (a + b)/2
- Variance: σ² = (b - a)²/12
- Median: (a + b)/2
- Mode: Any value in [a,b]
- Skewness: 0 (symmetric)
- Kurtosis: 9/5 (platykurtic)
Discrete Uniform
- PMF: P(X = x) = 1/n for each x in {x₁, ..., xₙ}
- Mean: (x₁ + xₙ)/2
- Variance: (n² - 1)/12 where n is number of values

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform

class UniformDistribution:
    def __init__(self, a=0, b=1):
        self.a = a
        self.b = b
        self.mean = (a + b) / 2
        self.variance = (b - a)**2 / 12
        self.std = np.sqrt(self.variance)

    def pdf(self, x):
        """Probability Density Function"""
        return np.where((x >= self.a) & (x <= self.b),
                       1/(self.b - self.a), 0)

    def cdf(self, x):
        """Cumulative Distribution Function"""
        return np.clip((x - self.a)/(self.b - self.a), 0, 1)

    def simulate(self, n_samples):
        """Generate random samples"""
        return np.random.uniform(self.a, self.b, n_samples)

# Visualization of PDF and CDF
def plot_uniform_distribution(a=0, b=1):
    dist = UniformDistribution(a, b)
    x = np.linspace(a-0.5, b+0.5, 1000)

    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))

    # PDF
    ax1.plot(x, dist.pdf(x))
    ax1.fill_between(x, dist.pdf(x), alpha=0.3)
    ax1.set_title('Probability Density Function')
    ax1.grid(True)

    # CDF
    ax2.plot(x, dist.cdf(x))
    ax2.set_title('Cumulative Distribution Function')
    ax2.grid(True)

    plt.tight_layout()
    plt.show()

plot_uniform_distribution(0, 1)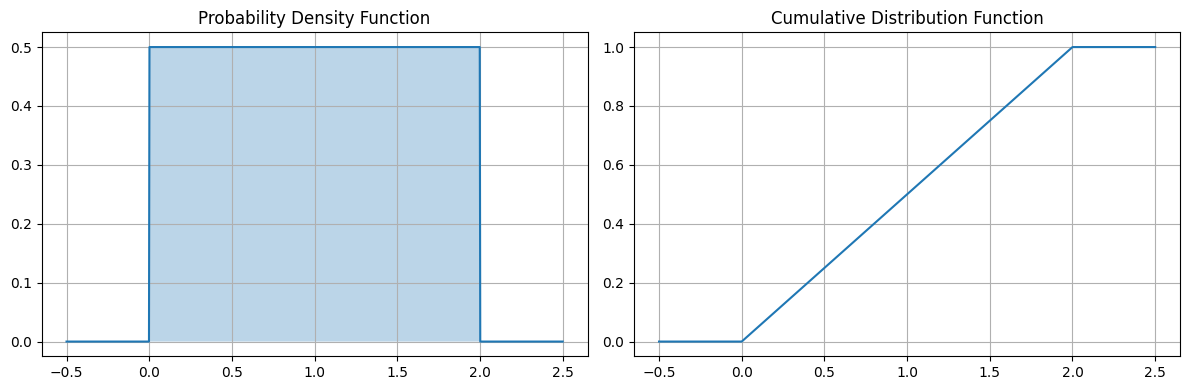

Uniform Distribution

Applications and Examples

Random Number Generation

def random_number_generator(a, b, n=1):
    """Generate n random numbers between a and b"""
    uniform = UniformDistribution(a, b)
    return uniform.simulate(n)

# Generate 5 random numbers between 0 and 10
numbers = random_number_generator(0, 10, 5)
print(f"Random numbers: {numbers}")

Simulation of Wait Times

class ServiceSimulator:
    def __init__(self, min_time=5, max_time=15):
        self.uniform = UniformDistribution(min_time, max_time)

    def simulate_service_times(self, n_customers):
        times = self.uniform.simulate(n_customers)
        return {
            'times': times,
            'average_wait': np.mean(times),
            'total_time': np.sum(times)
        }

# Simulate service times for 10 customers
simulator = ServiceSimulator()
results = simulator.simulate_service_times(10)
print(f"Average wait time: {results['average_wait']:.2f} minutes")
// Average wait time: 10.21 minutes

Quality Control Bounds

class QualityControl:
    def __init__(self, target, tolerance):
        self.lower = target - tolerance
        self.upper = target + tolerance
        self.uniform = UniformDistribution(self.lower, self.upper)

    def check_production(self, n_items):
        measurements = self.uniform.simulate(n_items)
        in_spec = np.logical_and(
            measurements >= self.lower,
            measurements <= self.upper
        )
        return {
            'measurements': measurements,
            'pass_rate': np.mean(in_spec),
            'failures': np.sum(~in_spec)

# Check 100 items with target 10 and tolerance ±0.5
qc = QualityControl(target=10, tolerance=0.5)
inspection = qc.check_production(100)
print(f"Pass rate: {inspection['pass_rate']:.1%}")
// Pass rate: 100.0%

Statistical Properties and Relationships

Sum of Uniform Variables
- Sum tends toward normal distribution (CLT)
- Special case: Irwin-Hall distribution
Order Statistics
- Minimum: a + (b-a)U₁/₍ₙ₊₁₎
- Maximum: a + (b-a)Uₙ/₍ₙ₊₁₎
- Where U follows Beta distribution

def demonstrate_sum_convergence(n_vars=12, n_samples=1000):
    """Demonstrate convergence to normal as we sum uniforms"""
    sums = np.sum([np.random.uniform(0, 1, n_samples)
                   for _ in range(n_vars)], axis=0)

    plt.figure(figsize=(8, 4))
    plt.hist(sums, bins=30, density=True)
    plt.title(f'Sum of {n_vars} Uniform Variables')
    plt.xlabel('Sum')
    plt.ylabel('Density')
    return plt

demonstrate_sum_convergence()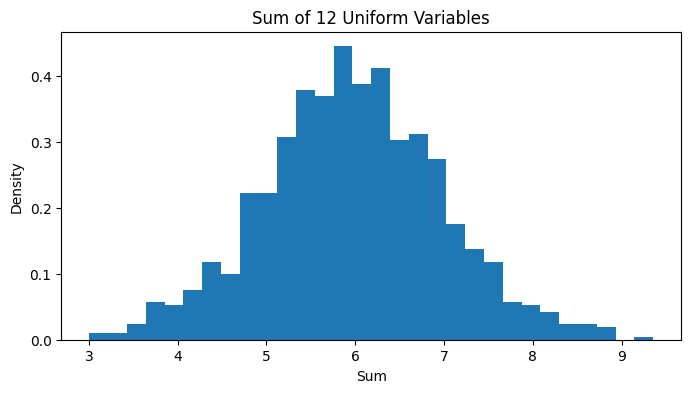

Sum of Uniform Variables

Hypothesis Testing with Uniform Distribution

The uniform distribution is often used in:

Testing random number generators
Goodness-of-fit tests
P-value calculations

def test_uniformity(data, alpha=0.05):
    """
    Kolmogorov-Smirnov test for uniformity
    """
    from scipy import stats

    ks_stat, p_value = stats.kstest(data, 'uniform')
    return {
        'statistic': ks_stat,
        'p_value': p_value,
        'uniform': p_value > alpha
    }

# Test random numbers for uniformity
data = np.random.uniform(0, 1, 1000)
results = test_uniformity(data)
print(f"Uniformity test p-value: {results['p_value']:.3f}")
// Uniformity test p-value: 0.999

Key Points and Best Practices

When to Use
- Random sampling
- Simple probability models
- Null hypothesis testing
- Initial approximations
Limitations
- Assumes equal probability
- May oversimplify real phenomena
- Sensitive to interval bounds
Common Mistakes
- Assuming uniformity without testing
- Ignoring boundary effects
- Misinterpreting discrete vs continuous

Log Normal Distribution

A Log Normal Distribution describes data where taking the natural log (ln) of the values gives a normal distribution. Think of it as a “skewed bell curve” that can’t go below zero.

Why It’s Important

Models things that grow by percentage (like money or populations)
Always positive (can’t have negative values)
Shows up naturally in many real-world situations

Key Features

Skewed right (long tail on right side)
Can’t be negative
Most values cluster near the left
Has a few very large values on the right

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import lognorm

# Create simple example data
normal_data = np.random.normal(0, 0.5, 1000)
lognormal_data = np.exp(normal_data)  # Transform to lognormal

# Plot both to show relationship
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# Normal distribution plot
ax1.hist(normal_data, bins=30, density=True)
ax1.set_title('Normal Distribution')
ax1.set_xlabel('Value')

# Log normal distribution plot
ax2.hist(lognormal_data, bins=30, density=True)
ax2.set_title('Log Normal Distribution')
ax2.set_xlabel('Value')

plt.tight_layout()
plt.show()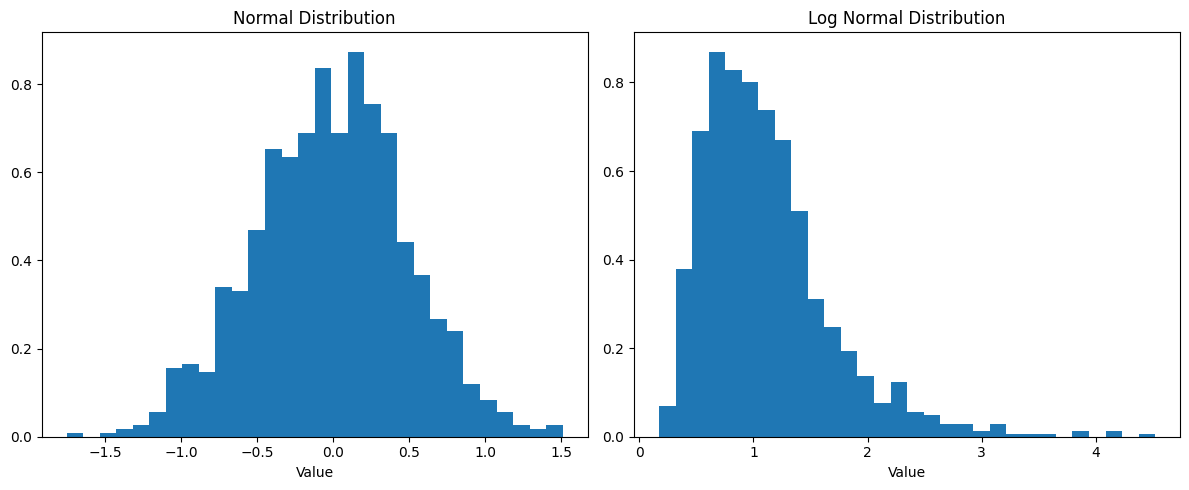

Log Normal Distribution

Real-World Examples

House Prices

def simulate_house_prices(median_price=300000, spread=0.5, n_houses=1000):
    """Simulate house prices in a city"""
    mu = np.log(median_price)  # Convert median to log scale
    prices = np.random.lognormal(mu, spread, n_houses)

    return {
        'median': np.median(prices),
        'mean': np.mean(prices),
        'cheapest': np.min(prices),
        'most_expensive': np.max(prices)
    }

# Example
prices = simulate_house_prices()
print(f"Median house: ${prices['median']:,.0f}")
print(f"Average house: ${prices['mean']:,.0f}")
print(f"Price range: ${prices['cheapest']:,.0f} to ${prices['most_expensive']:,.0f}")
// Median house: $293,919
// Average house: $334,266
// Price range: $54,054 to $1,700,471

Investment Growth

def investment_scenarios(initial=10000, years=30, risk=0.15):
    """Simulate possible investment outcomes"""
    annual_return = 0.07  # 7% average return

    # Generate 1000 possible scenarios
    final_amounts = initial * np.random.lognormal(
        (annual_return - risk**2/2) * years,
        risk * np.sqrt(years),
        1000
    )

    return {
        'median': np.median(final_amounts),
        'worst_10': np.percentile(final_amounts, 10),
        'best_10': np.percentile(final_amounts, 90)
    }

# Example
results = investment_scenarios()
print(f"Typical outcome: ${results['median']:,.0f}")
print(f"Range: ${results['worst_10']:,.0f} to ${results['best_10']:,.0f}")
// Typical outcome: $60,900
// Range: $19,375 to $173,670

When to Use It

Use log normal when your data:

Can’t be negative (like prices or sizes)
Is skewed right (has a long tail to the right)
Grows by percentages rather than fixed amounts

Simple Rules of Thumb

Most values will be below the mean
Median is less than mean
A few very large values will pull the mean up
Multiplying/dividing by a constant shifts the distribution

Common Mistakes to Avoid

Using it for negative values (impossible)
Expecting symmetry (it’s always skewed)
Using regular averages (use geometric mean instead)
Forgetting to transform back from log scale

# Example showing common statistics
def log_normal_stats(data):
    """Calculate key statistics for log-normal data"""
    log_data = np.log(data)

    return {
        'median': np.exp(np.mean(log_data)),  # Geometric mean
        'mean': np.mean(data),                # Arithmetic mean
        'typical_range': [
            np.exp(np.mean(log_data) - np.std(log_data)),
            np.exp(np.mean(log_data) + np.std(log_data))
        ]
    }

# Example with salary data
salaries = np.random.lognormal(11, 0.5, 1000)  # Generate sample salaries
stats = log_normal_stats(salaries)

print(f"Typical salary (median): ${stats['median']:,.0f}")
print(f"Average salary (mean): ${stats['mean']:,.0f}")
print(f"Typical range: ${stats['typical_range'][0]:,.0f} to ${stats['typical_range'][1]:,.0f}")
// Typical salary (median): $31,623
// Average salary (mean): $34,859
// Typical range: $25,262 to $41,771

Remember: Log normal distributions are perfect for things that grow by percentages (like money) or can’t be negative (like sizes or times).

Power Law Distribution/Pareto Distribution

The Power Law Distribution (also known as Pareto Distribution) describes situations where a small number of items dominate the majority of outcomes. It’s often called the “80/20 rule” - where 80% of effects come from 20% of causes.

Key Properties

Long tail distribution (many small values, few very large ones)
No typical scale (looks similar at different scales)
Formula: P(x) ∝ x^(-α) where α > 0
Common α values: 2-3 for natural phenomena

Real-World Examples

Wealth distribution (few people own most wealth)
City populations (few cities have most people)
Website traffic (few pages get most visits)
Social media followers (few accounts have most followers)

import numpy as np
import matplotlib.pyplot as plt

def plot_power_law(alpha=2, n_samples=1000):
    # Generate power law data
    x = np.random.pareto(alpha, n_samples) + 1

    # Plot on log-log scale
    plt.figure(figsize=(10, 6))
    plt.hist(x, bins=50, density=True, alpha=0.7)
    plt.yscale('log')
    plt.xscale('log')
    plt.title(f'Power Law Distribution (α={alpha})')
    plt.xlabel('Value (log scale)')
    plt.ylabel('Frequency (log scale)')
    plt.grid(True)
    return plt

# Example usage
plot_power_law()
plt.show()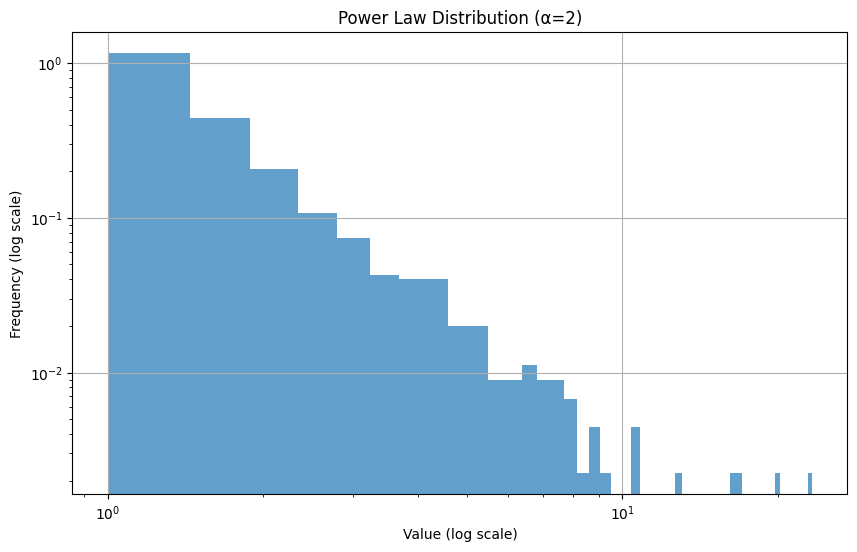

Power Law Distribution

Simple Example: Website Traffic

def simulate_website_traffic(n_pages=100):
    """Simulate daily views for website pages"""
    # Generate power law distributed views
    views = np.random.pareto(2, n_pages) * 100

    # Sort and analyze
    sorted_views = np.sort(views)[::-1]  # Descending order
    total_views = np.sum(views)

    # Find 80/20 point
    cumsum = np.cumsum(sorted_views)
    pages_for_80 = np.searchsorted(cumsum, 0.8 * total_views) + 1

    return {
        'top_pages': sorted_views[:5],
        'pages_for_80_percent': pages_for_80,
        'percent_pages': (pages_for_80 / n_pages) * 100
    }

# Example
traffic = simulate_website_traffic()
print(f"Top 5 page views: {traffic['top_pages'].astype(int)}")
print(f"{traffic['pages_for_80_percent']} pages ({traffic['percent_pages']:.1f}%) "
      f"generate 80% of traffic")
// Top 5 page views: [449 396 388 277 272]
// 40 pages (40.0%) generate 80% of traffic

When to Use

Analyzing extreme inequalities
Modeling natural phenomena
Risk assessment
Network analysis

Key Points

No “typical” or “average” value
Extreme values are more common than in normal distribution
Often indicates self-reinforcing processes
Important for risk management (extreme events more likely)

Note: Power laws appear in many natural and social systems. If you see huge differences between largest and smallest values, consider using a power law distribution.

Inferential Statistics

Estimates

Estimates are predictions or approximations of unknown values in data science. They help us make informed decisions based on available data.

Types of Estimates

Point Estimate
- Single value prediction
- Example: Sample mean (x̄) estimates population mean (μ)
```
data = [1, 2, 3, 4, 5]
point_estimate = np.mean(data)  # = 3
```

Interval Estimate

Range of likely values
Common form: Confidence Intervals

def confidence_interval(data, confidence=0.95):
    mean = np.mean(data)
    std = np.std(data, ddof=1)
    margin = 1.96 * (std / np.sqrt(len(data)))  # 95% CI
    return mean - margin, mean + margin

Common Estimators

Mean (Average)
- Estimates central tendency
- Best for symmetric data
```
mean = sum(data) / len(data)
```
Median
- Estimates central value
- Better for skewed data
```
median = sorted(data)[len(data)//2]
```

Sample Variance

Estimates data spread
Uses n-1 for unbiased estimate

variance = sum((x - mean)**2 for x in data) / (len(data) - 1)

Properties of Good Estimators

Unbiased
- Average estimate equals true value
- Example: Sample mean is unbiased
Consistent
- More data = better estimate
- Example: Law of large numbers
Efficient
- Minimum variance among similar estimators
- Example: Sample mean vs single observation

Real-World Example

class SalesEstimator:
    def __init__(self, sales_data):
        self.data = sales_data

    def daily_estimate(self):
        mean = np.mean(self.data)
        ci = confidence_interval(self.data)
        return {
            'point_estimate': mean,
            'confidence_interval': ci,
            'reliability': 'High' if (ci[1]-ci[0]) < mean*0.2 else 'Low'
        }

# Usage
sales = [100, 120, 80, 95, 110, 105, 90]
estimator = SalesEstimator(sales)
forecast = estimator.daily_estimate()
print(f"Expected sales: {forecast['point_estimate']:.0f}")
print(f"Range: {forecast['confidence_interval'][0]:.0f} to {forecast['confidence_interval'][1]:.0f}")
// Expected sales: 100
// Range: 90 to 110

Key Point: Choose estimators based on your data type and what you’re trying to predict.

Hypothesis Testing

Hypothesis testing is a method to make decisions about a population using sample data. It helps determine if an observed effect is statistically significant.

Basic Steps

State Hypotheses
- Null (H₀): No effect/relationship exists
- Alternative (H₁): Effect/relationship exists
Choose Significance Level (α)
- Usually 0.05 (5%)
- Represents acceptable false positive rate
Calculate Test Statistic
- Based on sample data
- Common tests: z-test, t-test
Compare p-value
- If p < α: Reject H₀
- If p ≥ α: Fail to reject H₀

Simple Example

from scipy import stats

# Test if mean score is different from 70
scores = [72, 75, 68, 77, 69, 71, 74, 73]

# Run t-test
t_stat, p_value = stats.ttest_1samp(scores, 70)

print(f"p-value: {p_value:.4f}")
if p_value < 0.05:
    print("Reject null hypothesis")
else:
    print("Fail to reject null hypothesis")

// p-value: 0.0615
// Fail to reject null hypothesis

Common Tests

One-Sample t-test

Compare sample mean to known value

def one_sample_ttest(data, expected_mean, alpha=0.05):
    t_stat, p_val = stats.ttest_1samp(data, expected_mean)
    return {
        'p_value': p_val,
        'significant': p_val < alpha,
        'test_stat': t_stat
    }

Two-Sample t-test

Compare means of two groups

def two_sample_ttest(group1, group2, alpha=0.05):
    t_stat, p_val = stats.ttest_ind(group1, group2)
    return {
        'p_value': p_val,
        'significant': p_val < alpha,
        'test_stat': t_stat
    }

Chi-Square Test

Test categorical data relationships

def chi_square_test(observed, expected, alpha=0.05):
    chi2, p_val = stats.chisquare(observed, expected)
    return {
        'p_value': p_val,
        'significant': p_val < alpha,
        'test_stat': chi2
    }

Real-World Example

class DrugEffectTest:
    def __init__(self, treatment_group, control_group):
        self.treatment = treatment_group
        self.control = control_group

    def analyze(self):
        # Run t-test
        result = two_sample_ttest(self.treatment, self.control)

        # Calculate effect size
        effect = np.mean(self.treatment) - np.mean(self.control)

        return {
            'significant': result['significant'],
            'p_value': result['p_value'],
            'effect_size': effect,
            'recommendation': 'Use drug' if (result['significant'] and effect > 0)
                            else 'Need more research'
        }

# Example usage
treatment = [75, 82, 78, 80, 79]  # Drug group
control = [70, 71, 73, 69, 72]    # Placebo group

test = DrugEffectTest(treatment, control)
result = test.analyze()

print(f"Effect: {result['effect_size']:.1f} units")
print(f"P-value: {result['p_value']:.4f}")
print(f"Recommendation: {result['recommendation']}")
// Effect: 7.8 units
// P-value: 0.0004
// Recommendation: Use drug

Common Mistakes to Avoid

P-value Misinterpretation
- P-value is NOT probability H₀ is true
- Only shows how rare data is under H₀
Multiple Testing
- More tests = higher chance of false positives
- Use Bonferroni correction: α/n for n tests
Sample Size Issues
- Too small: May miss real effects
- Too large: May find tiny, meaningless effects

Key Point: Hypothesis testing helps make decisions but should be used with context and common sense.

P Value

P-value helps determine if a result is statistically significant. Think of it as “how surprising is this result if there was no real effect?”

Key Points

Smaller p-value = stronger evidence against null hypothesis
Common threshold: p < 0.05 (5% significance level)
Range: 0 to 1 (0% to 100% probability)

Simple Example

from scipy import stats
import numpy as np

# Test if coin is fair
flips = [1, 1, 1, 1, 1, 1, 1, 0, 0, 0]  # 1=heads, 0=tails
heads = sum(flips)
total = len(flips)

# Calculate p-value (two-tailed test)
result = stats.binomtest(heads, total, p=0.5)
p_value = result.pvalue

# Print results
print(f"Number of heads: {heads} out of {total}")
print(f"P-value: {p_value:.3f}")
print(f"Interpretation: {'Reject null hypothesis' if p_value < 0.05 else 'Fail to reject null hypothesis'}")

# In this case:
# H0: Coin is fair (p = 0.5)
# H1: Coin is biased (p ≠ 0.5)
# Since p-value (0.344) > 0.05, we fail to reject H0

// Number of heads: 7 out of 10
// P-value: 0.344
// Interpretation: Fail to reject null hypothesis

Interpretation Guide

p < 0.01: Very strong evidence
p < 0.05: Strong evidence
p < 0.10: Weak evidence
p ≥ 0.10: No evidence

Common Mistakes

P-value is NOT:
- Probability null hypothesis is true
- Probability of being wrong
- Effect size or importance
Small p-value doesn’t mean:
- Large effect
- Practical significance
- Reproducible results

Remember: P-value measures evidence strength, not effect size or practical importance

Z Test

A Z-test is a statistical test used to determine if there’s a significant difference between a sample mean and a population mean when:

Population standard deviation is known
Sample size is large (n > 30)

Formula

z = (x̄ - μ) / (σ / √n)

where:
x̄ = sample mean
μ = population mean
σ = population standard deviation
n = sample size

Simple Example

import numpy as np
from scipy import stats

def z_test(sample, pop_mean, pop_std):
    """
    Perform one-sample z-test

    Args:
        sample: List of sample values
        pop_mean: Known population mean
        pop_std: Known population standard deviation
    """
    n = len(sample)
    sample_mean = np.mean(sample)
    z_score = (sample_mean - pop_mean) / (pop_std / np.sqrt(n))
    p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))  # Two-tailed test

    return {
        'z_score': z_score,
        'p_value': p_value,
        'significant': p_value < 0.05
    }

# Example: Test if class scores are different from population
scores = [85, 88, 92, 78, 90, 87, 86, 84, 89, 91]  # Sample scores
pop_mean = 82  # Known population mean
pop_std = 5    # Known population standard deviation

result = z_test(scores, pop_mean, pop_std)
print(f"Z-score: {result['z_score']:.2f}")
print(f"P-value: {result['p_value']:.4f}")
print(f"Significant? {result['significant']}")

// Z-score: 3.16
// P-value: 0.0016
// Significant? True

When to Use Z-Test

Large sample size (n > 30)
Known population standard deviation
Testing means (not proportions)
Data is normally distributed

Real-World Example: Quality Control

class ProductQuality:
    def __init__(self, target_weight=100, pop_std=2):
        self.target = target_weight
        self.pop_std = pop_std

    def test_batch(self, measurements):
        result = z_test(measurements, self.target, self.pop_std)
        return {
            'pass': not result['significant'],  # Pass if no significant difference
            'z_score': result['z_score'],
            'p_value': result['p_value']
        }

# Test a batch of products
weights = [101, 99, 100, 102, 98, 101, 99, 100, 101, 102]
qc = ProductQuality()
test = qc.test_batch(weights)

print(f"Batch {'passed' if test['pass'] else 'failed'} quality check")
print(f"Z-score: {test['z_score']:.2f}")

// Batch passed quality check
// Z-score: 0.47

Key Points

Assumptions
- Normal distribution
- Independent samples
- Known population standard deviation
Interpretation
- |Z| > 1.96: Significant at 5% level
- |Z| > 2.58: Significant at 1% level
- Larger |Z| = stronger evidence
Limitations
- Requires known population std
- Not good for small samples
- Assumes normality

Note: If population standard deviation is unknown or sample size is small, use t-test instead.

Student’s t Distribution

The Student’s t Distribution is similar to the normal distribution but has heavier tails. It’s used when:

Sample size is small (n < 30)
Population standard deviation is unknown

Key Points

Shape depends on degrees of freedom (df = n-1)
Approaches normal distribution as df increases
Used for t-tests and confidence intervals

Formula

from scipy import stats
import numpy as np

def t_distribution(df, x):
    """Calculate t-distribution probability density"""
    return stats.t.pdf(x, df)

Example: Compare t vs Normal

import matplotlib.pyplot as plt

# Create comparison plot
x = np.linspace(-4, 4, 100)
df_values = [1, 5, 30]

plt.figure(figsize=(10, 6))
for df in df_values:
    plt.plot(x, stats.t.pdf(x, df),
             label=f't (df={df})')

plt.plot(x, stats.norm.pdf(x),
         label='Normal', linestyle='--')
plt.title('t Distribution vs Normal')
plt.legend()
plt.grid(True)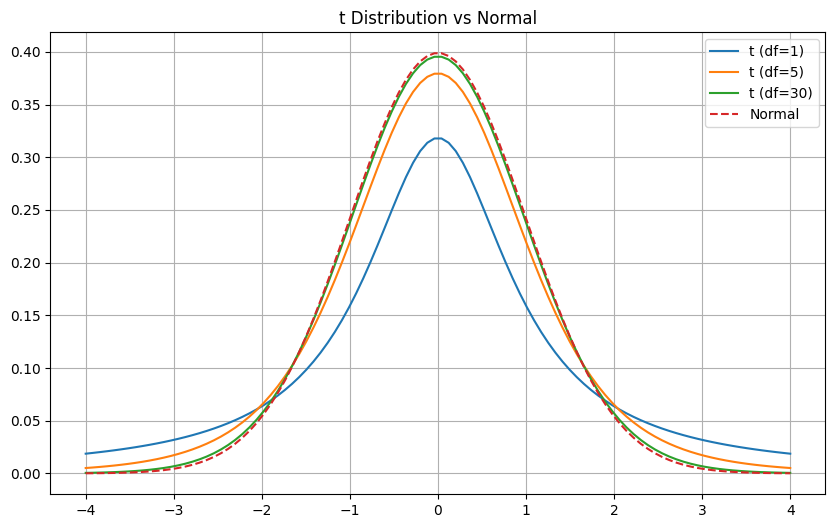

t Distribution vs Normal

Common Uses

Small Sample Testing

def t_test(sample, pop_mean):
    """One-sample t-test"""
    t_stat, p_value = stats.ttest_1samp(sample, pop_mean)
    return {
        't_statistic': t_stat,
        'p_value': p_value,
        'significant': p_value < 0.05
    }

# Example
data = [25, 28, 29, 30, 31]
result = t_test(data, 27)
print(f"P-value: {result['p_value']:.4f}")

// P-value: 0.1951

Confidence Intervals

def confidence_interval(data, confidence=0.95):
    """Calculate confidence interval"""
    n = len(data)
    mean = np.mean(data)
    sem = stats.sem(data)  # Standard error of mean
    interval = stats.t.interval(confidence, n-1, mean, sem)
    return interval

# Example
data = [10, 12, 11, 13, 9]
ci = confidence_interval(data)
print(f"95% CI: ({ci[0]:.1f}, {ci[1]:.1f})")

// 95% CI: (9.0, 13.0)

When to Use

Small sample sizes
Unknown population standard deviation
Testing means or differences
Creating confidence intervals

Key Differences from Normal Distribution

More spread out (heavier tails)
Changes shape with sample size
More conservative (wider intervals)
Better for small samples

Note: As sample size increases (n > 30), t-distribution becomes very close to normal distribution.

T-Stats with T-test Hypothesis Testing

T-tests help determine if there’s a significant difference between means. They’re especially useful when working with small samples (n < 30).

Basic Types of T-tests

One-Sample T-test

Compares sample mean to known value

from scipy import stats

# Example: Test if student scores differ from target (75)
scores = [72, 78, 75, 80, 73]
t_stat, p_value = stats.ttest_1samp(scores, 75)

Independent T-test

Compares means of two independent groups

# Compare treatment vs control
treatment = [75, 82, 78, 80]
control = [70, 71, 73, 69]
t_stat, p_value = stats.ttest_ind(treatment, control)

Paired T-test

Compares before/after measurements

# Compare before/after scores
before = [70, 72, 71, 73]
after = [75, 78, 77, 76]
t_stat, p_value = stats.ttest_rel(before, after)

Simple Example with Explanation

def run_ttest(sample_data, expected_mean=0, alpha=0.05):
    """
    Run one-sample t-test

    Args:
        sample_data: List of values
        expected_mean: Value to test against
        alpha: Significance level
    """
    # Calculate t-statistic and p-value
    t_stat, p_value = stats.ttest_1samp(sample_data, expected_mean)

    return {
        't_statistic': t_stat,
        'p_value': p_value,
        'significant': p_value < alpha,
        'mean_difference': np.mean(sample_data) - expected_mean
    }

# Example usage
scores = [85, 82, 88, 84, 86]
result = run_ttest(scores, expected_mean=80)

print(f"T-statistic: {result['t_statistic']:.2f}")
print(f"P-value: {result['p_value']:.4f}")
print(f"Mean difference: {result['mean_difference']:.1f}")
print(f"Significant? {result['significant']}")

// T-statistic: 5.00
// P-value: 0.0075
// Mean difference: 5.0
// Significant? True

When to Use Each Test

One-Sample T-test
- Testing against known value
- Example: Are test scores different from 70?
Independent T-test
- Comparing two separate groups
- Example: Does treatment group differ from control?
Paired T-test
- Before/after measurements
- Example: Did training improve scores?

Interpreting Results

T-statistic
- Larger = stronger evidence
- Sign shows direction (positive/negative)
P-value
- < 0.05: Statistically significant
- ≥ 0.05: Not significant
Effect Size
- Mean difference shows practical significance
- Consider alongside p-value

Common Mistakes to Avoid

Don’t ignore assumptions:
- Normal distribution
- Independent samples
- Equal variances (for independent t-test)

Don’t rely only on p-values:

def analyze_results(result):
    """Better interpretation of t-test"""
    return {
        'statistical_sig': result['p_value'] < 0.05,
        'practical_sig': abs(result['mean_difference']) > 5,
        'recommendation': 'Consider both statistical and practical significance'
    }

Real-World Example

class DrugEffectiveness:
    def __init__(self, treatment_data, control_data):
        self.treatment = treatment_data
        self.control = control_data

    def analyze(self):
        # Run t-test
        t_stat, p_val = stats.ttest_ind(self.treatment, self.control)

        # Calculate effect size
        effect = np.mean(self.treatment) - np.mean(self.control)

        return {
            't_statistic': t_stat,
            'p_value': p_val,
            'effect_size': effect,
            'recommendation': 'Effective' if (p_val < 0.05 and effect > 0)
                            else 'Not effective'
        }

# Example usage
treatment = [95, 92, 98, 94, 96]  # Drug group
control = [85, 87, 88, 86, 84]    # Placebo group

study = DrugEffectiveness(treatment, control)
results = study.analyze()

print(f"Effect size: {results['effect_size']:.1f} units")
print(f"P-value: {results['p_value']:.4f}")
print(f"Recommendation: {results['recommendation']}")

// Effect size: 9.0 units
// P-value: 0.0001
// Recommendation: Effective

Key Points:

Use t-tests for small samples

Consider both p-value and effect size

Check assumptions before testing

Interpret results in context

T-test vs Z-test

T-tests and Z-tests are both used to compare means, but they have different use cases and assumptions.

Quick Reference

Feature	Z-test	T-test
Sample Size	Large (n > 30)	Any size
Population σ	Must be known	Can be unknown
Distribution	Normal	Student’s t
Tail Weight	Light tails	Heavy tails

Simple Example

import numpy as np
from scipy import stats

def choose_test(sample, pop_mean, pop_std=None):
    """
    Choose and run appropriate test

    Args:
        sample: Data to test
        pop_mean: Population mean to test against
        pop_std: Population standard deviation (if known)
    """
    n = len(sample)

    if n > 30 and pop_std is not None:
        # Use Z-test
        z_score = (np.mean(sample) - pop_mean) / (pop_std / np.sqrt(n))
        p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))
        test_type = 'Z-test'
        stat = z_score
    else:
        # Use T-test
        stat, p_value = stats.ttest_1samp(sample, pop_mean)
        test_type = 'T-test'

    return {
        'test_type': test_type,
        'statistic': stat,
        'p_value': p_value
    }

# Example usage
small_sample = [75, 82, 78, 80, 79]  # n = 5
large_sample = np.random.normal(75, 5, 50)  # n = 50
pop_std = 5

# Test both samples
small_result = choose_test(small_sample, 70)
large_result = choose_test(large_sample, 70, pop_std)

print(f"Small sample: {small_result['test_type']}")
print(f"Large sample: {large_result['test_type']}")

// Small sample: T-test
// Large sample: Z-test

When to Use Each Test

Use Z-test when:
- Large sample (n > 30)
- Known population standard deviation
- Need exact probability values
Use T-test when:
- Small sample size
- Unknown population standard deviation
- Working with sample statistics

Key Differences

Tail Weight
- Z-test: Lighter tails (normal distribution)
- T-test: Heavier tails (more conservative)
Critical Values
- Z-test: Fixed values (e.g., ±1.96 for 95%)
- T-test: Varies with sample size (degrees of freedom)
Confidence Intervals

def compare_intervals(data, pop_std=None, confidence=0.95):
    """Compare Z and T confidence intervals"""
    n = len(data)
    mean = np.mean(data)

    # Z interval (if pop_std known)
    if pop_std:
        z = stats.norm.ppf((1 + confidence) / 2)
        z_margin = z * (pop_std / np.sqrt(n))
        z_interval = (mean - z_margin, mean + z_margin)

    # T interval
    t_interval = stats.t.interval(confidence, n-1, mean, stats.sem(data))

    return {
        'z_interval': z_interval if pop_std else None,
        't_interval': t_interval
    }

Best Practices

Default to T-test unless you:
- Have large sample AND
- Know population standard deviation
Consider Sample Size
- Small (n < 30): Always use t-test
- Large (n > 30): Either test works
Check Assumptions
- Normal distribution
- Independent observations
- Random sampling

Note: When in doubt, use t-test. It’s more conservative and safer for most situations.

Type I and Type II Errors

Type I and Type II errors are fundamental concepts in hypothesis testing that help us understand the two ways we can make mistakes.

Quick Reference

Error Type	Definition	Common Name	Example
Type I	Rejecting true null hypothesis	False Positive	Convicting innocent person
Type II	Failing to reject false null hypothesis	False Negative	Missing actual disease

Simple Example

import numpy as np
from scipy import stats

def test_with_errors(data, null_mean, alpha=0.05):
    """
    Run hypothesis test and explain possible errors

    Args:
        data: Sample data
        null_mean: Null hypothesis mean
        alpha: Significance level (Type I error rate)
    """
    # Run t-test
    t_stat, p_value = stats.ttest_1samp(data, null_mean)

    # Decision
    reject_null = p_value < alpha

    # Explain possible errors
    if reject_null:
        error_type = "Type I error possible (false positive)"
    else:
        error_type = "Type II error possible (false negative)"

    return {
        'p_value': p_value,
        'reject_null': reject_null,
        'possible_error': error_type
    }

# Example
scores = [75, 82, 78, 80, 79]
result = test_with_errors(scores, null_mean=70)
print(f"Decision: {'Reject' if result['reject_null'] else 'Fail to reject'} null")
print(f"Possible error: {result['possible_error']}")

// Decision: Reject null
// Possible error: Type I error possible (false positive)

Key Concepts

Type I Error (α)
- Rejecting H₀ when it’s true
- Probability = significance level (α)
- Usually set to 0.05 (5%)
- More serious in legal/medical contexts
Type II Error (β)
- Not rejecting H₀ when it’s false
- Related to test power (1 - β)
- Affected by:
  - Sample size
  - Effect size
  - Significance level

Real-World Example: Medical Test

class MedicalTest:
    def __init__(self, sensitivity=0.95, specificity=0.98):
        self.sensitivity = sensitivity  # True Positive Rate
        self.specificity = specificity # True Negative Rate

    def test_patient(self, has_disease, n_tests=1000):
        """Simulate medical tests"""
        if has_disease:
            # Type II error rate = 1 - sensitivity
            false_negatives = np.random.binomial(n_tests, 1-self.sensitivity)
            return {
                'condition': 'Sick',
                'errors': false_negatives,
                'error_type': 'Type II',
                'error_rate': false_negatives/n_tests
            }
        else:
            # Type I error rate = 1 - specificity
            false_positives = np.random.binomial(n_tests, 1-self.specificity)
            return {
                'condition': 'Healthy',
                'errors': false_positives,
                'error_type': 'Type I',
                'error_rate': false_positives/n_tests
            }

# Example usage
test = MedicalTest()
sick_results = test.test_patient(has_disease=True)
healthy_results = test.test_patient(has_disease=False)

print(f"Type II Error Rate (missed disease): {sick_results['error_rate']:.1%}")
print(f"Type I Error Rate (false alarms): {healthy_results['error_rate']:.1%}")

// Type II Error Rate (missed disease): 5.7%
// Type I Error Rate (false alarms): 2.2%

Trade-offs

Error Rate Relationship
- Decreasing α increases β
- Decreasing β increases α
- Can’t minimize both simultaneously
Practical Considerations
- Cost of each error type
- Available sample size
- Required confidence level

Common Mistakes to Avoid

Not Considering Both Errors

def assess_test_quality(alpha, beta):
    """Evaluate overall test quality"""
    power = 1 - beta
    return {
        'false_positive_rate': alpha,
        'false_negative_rate': beta,
        'power': power,
        'quality': 'Good' if (alpha < 0.05 and power > 0.8) else 'Poor'
    }

Focusing Only on Significance
- Consider practical significance
- Balance both error types
- Account for sample size

Key Point: Always consider both error types and their real-world implications when making decisions based on statistical tests.

Conclusion

Understanding Type I and Type II errors is crucial for making informed decisions in data analysis. By balancing these errors, we can improve the reliability and practicality of our statistical tests.

Remember, the goal is not to minimize errors, but to make informed decisions with the best possible information.

Summary

Type I Error: Rejecting true null hypothesis
Type II Error: Failing to reject false null hypothesis
Trade-offs: Can’t minimize both simultaneously
Practical Considerations: Cost, sample size, confidence level
Common Mistakes: Focusing only on significance

Key Point: Always consider both error types and their real-world implications when making decisions based on statistical tests.

Bayesian Statistics

Bayesian statistics is an approach that updates beliefs based on new evidence. It uses probability to express uncertainty about events and parameters.

Key Concepts

Prior Probability (Prior)
- Initial belief before new data
- Based on previous knowledge
Likelihood
- Probability of data given parameters
- How well parameters explain data
Posterior Probability
- Updated belief after seeing data
- Combines prior and likelihood

Bayes’ Theorem

The fundamental formula:

P(A|B) = P(B|A) * P(A) / P(B)

where:
P(A|B) = Posterior
P(B|A) = Likelihood
P(A) = Prior
P(B) = Evidence

Simple Example

def bayes_update(prior_prob, likelihood, evidence):
    """Calculate posterior probability"""
    return (likelihood * prior_prob) / evidence

# Example: Disease testing
prior = 0.01      # 1% have disease
likelihood = 0.95 # Test 95% accurate for sick people
evidence = 0.05   # 5% test positive

posterior = bayes_update(prior, likelihood, evidence)
print(f"Probability of disease given positive test: {posterior:.1%}")
// Probability of disease given positive test: 19.0%

Real-World Applications

Spam Detection

class SpamFilter:
    def __init__(self):
        self.word_probs = {
            'money': 0.8,    # P(spam|word)
            'friend': 0.2,
            'buy': 0.7
        }
        self.spam_prior = 0.3  # 30% of emails are spam

    def classify(self, words):
        prob = self.spam_prior
        for word in words:
            if word in self.word_probs:
                prob *= self.word_probs[word]
        return prob > 0.5

# Example
filter = SpamFilter()
email = ['money', 'buy']
is_spam = filter.classify(email)
print(f"Email classified as: {'Spam' if is_spam else 'Not Spam'}")
// Email classified as: Not Spam

A/B Testing

def bayesian_ab_test(a_success, a_total, b_success, b_total):
    """Compare two versions using Bayesian approach"""
    from scipy import stats

    # Calculate success rates
    rate_a = a_success / a_total
    rate_b = b_success / b_total

    # Calculate confidence
    confidence = stats.beta(a_success + 1, a_total - a_success + 1).mean()

    return {
        'better_version': 'A' if rate_a > rate_b else 'B',
        'confidence': confidence,
        'recommend_switch': confidence > 0.95
    }

# Example
result = bayesian_ab_test(120, 1000, 150, 1000)
print(f"Better version: {result['better_version']}")
print(f"Confidence: {result['confidence']:.1%}")
// Better version: B
// Confidence: 98.2%

Advantages Over Frequentist Statistics

Intuitive Updates
- Naturally updates beliefs with new data
- Handles uncertainty better
Prior Knowledge
- Incorporates existing knowledge
- More realistic in real-world scenarios
Interpretable Results
- Gives probability distributions
- Easier to understand for decisions

Common Uses

Medical Diagnosis
- Update disease probability with test results
- Consider patient history (prior)
Machine Learning
- Parameter estimation
- Model uncertainty
- Neural network weights
Risk Assessment
- Financial decisions
- Project planning
- Insurance

Simple Implementation

class BayesianAnalyzer:
    def __init__(self, prior=0.5):
        self.prior = prior
        self.data = []

    def update(self, new_data, likelihood):
        """Update beliefs with new data"""
        posterior = (likelihood * self.prior) / (
            likelihood * self.prior +
            (1 - likelihood) * (1 - self.prior)
        )
        self.prior = posterior
        self.data.append(new_data)
        return posterior

    def get_confidence(self):
        return f"{self.prior:.1%}"

# Example usage
analyzer = BayesianAnalyzer()
print(f"Initial belief: {analyzer.get_confidence()}")

# Update with new evidence
evidence = [True, True, False, True]
for e in evidence:
    likelihood = 0.8 if e else 0.2
    analyzer.update(e, likelihood)

print(f"Updated belief: {analyzer.get_confidence()}")
// Initial belief: 50.0%
// Updated belief: 94.1%

Key Points to Remember

Start with Prior
- Use existing knowledge
- Be explicit about assumptions
Update with Data
- Use Bayes’ theorem
- Consider evidence strength
Make Decisions
- Use posterior probabilities
- Consider uncertainty

Note: Bayesian statistics helps make better decisions by combining prior knowledge with new evidence in a natural way.

Conclusion

Bayesian statistics is a powerful tool for making decisions based on uncertain data. It provides a natural way to update beliefs with new evidence and can be used in a wide range of applications.

By understanding the basics and practicing with real-world examples, you can start using Bayesian methods to improve your decision-making process.

Summary

Bayes’ Theorem: P(A|B) = P(B|A) * P(A) / P(B)
Prior: Initial belief
Likelihood: Data explanation
Posterior: Updated belief
Common Uses: Medical, ML, risk assessment

Key Point: Bayesian statistics helps make better decisions by combining prior knowledge with new evidence in a natural way.

Confidence Interval and Margin of Error

A confidence interval shows the likely range for a population value, while margin of error shows how far the estimate might be from the true value.

Simple Formula

margin_of_error = z_score * (standard_deviation / √sample_size)
confidence_interval = sample_mean ± margin_of_error

Basic Example

import numpy as np
from scipy import stats

def calculate_confidence_interval(data, confidence=0.95):
    """
    Calculate confidence interval for a dataset

    Args:
        data: List of numbers
        confidence: Confidence level (default 95%)
    """
    mean = np.mean(data)
    std_error = stats.sem(data)
    interval = stats.t.interval(confidence, len(data)-1, mean, std_error)

    return {
        'mean': mean,
        'lower': interval[0],
        'upper': interval[1],
        'margin': interval[1] - mean
    }

# Example usage
scores = [72, 75, 68, 77, 69, 71, 74, 73]
ci = calculate_confidence_interval(scores)
print(f"Mean: {ci['mean']:.1f}")
print(f"95% CI: ({ci['lower']:.1f}, {ci['upper']:.1f}")
print(f"Margin of Error: ±{ci['margin']:.1f}")

Common Confidence Levels

90% → z = 1.645
95% → z = 1.96 (most common)
99% → z = 2.576

Real-World Example: Survey Results

class SurveyAnalyzer:
    def __init__(self, responses, confidence=0.95):
        self.data = responses
        self.confidence = confidence

    def analyze(self):
        ci = calculate_confidence_interval(self.data, self.confidence)
        return {
            'estimate': ci['mean'],
            'margin': ci['margin'],
            'range': f"({ci['lower']:.1f} - {ci['upper']:.1f})",
            'reliability': 'High' if ci['margin'] < 5 else 'Low'
        }

# Example: Customer satisfaction scores (1-10)
scores = [8, 7, 9, 8, 8, 7, 9, 8, 7, 8]
survey = SurveyAnalyzer(scores)
results = survey.analyze()

print(f"Customer satisfaction: {results['estimate']:.1f} ± {results['margin']:.1f}")
print(f"Confidence range: {results['range']}")

Factors Affecting Margin of Error

Sample Size
- Larger sample = smaller margin
- Doubles sample size → reduces margin by √2
Confidence Level
- Higher confidence = larger margin
- 99% CI wider than 95% CI
Population Variability
- More variable data = larger margin
- Less consistent = less certain

Sample Size Calculator

def required_sample_size(margin_of_error, confidence=0.95, std_dev=0.5):
    """
    Calculate required sample size for desired margin of error

    Args:
        margin_of_error: Desired margin (as decimal)
        confidence: Confidence level (default 95%)
        std_dev: Estimated standard deviation
    """
    z = stats.norm.ppf((1 + confidence) / 2)
    n = ((z * std_dev) / margin_of_error) ** 2
    return int(np.ceil(n))

# Example: For ±3% margin at 95% confidence
sample_size = required_sample_size(0.03)
print(f"Required sample size: {sample_size}")

Key Points

Interpretation
- “We are 95% confident the true value is in this range”
- Not “95% of data falls in this range”
Trade-offs
- Narrower CI = Less confident
- Wider CI = More confident
- Balance precision vs certainty
Common Uses
- Polls and surveys
- Quality control
- Scientific research
- Medical studies

Best Practices

Report Both
- Always show mean and margin
- Example: 75.2 ± 3.4
Consider Context
- Is margin acceptable for decisions?
- What’s the cost of being wrong?
Sample Size
- Get enough data for desired precision
- Consider cost vs accuracy needs

Remember: Larger sample sizes give more precise estimates (smaller margins of error), but there’s always some uncertainty in real-world measurements.

Chi-Square Test

The Chi-Square Test helps determine if there’s a relationship between categorical variables or if observed data matches expected patterns.

Types of Chi-Square Tests

Independence Test
- Tests if two variables are related
- Example: Is gender related to voting preference?
Goodness of Fit
- Tests if data matches expected distribution
- Example: Are dice rolls fair?

Simple Example

from scipy import stats
import numpy as np

def chi_square_test(observed, expected=None):
    """
    Run chi-square test

    Args:
        observed: Observed frequencies
        expected: Expected frequencies (optional)
    """
    if expected is None:
        # Assume equal distribution
        expected = [sum(observed) / len(observed)] * len(observed)

    chi2, p_value = stats.chisquare(observed, expected)

    return {
        'chi_square': chi2,
        'p_value': p_value,
        'significant': p_value < 0.05
    }

# Example: Test if dice is fair
rolls = [10, 8, 12, 9, 11, 10]  # Frequencies of 1-6
result = chi_square_test(rolls)
print(f"P-value: {result['p_value']:.3f}")
print(f"Fair dice? {'No' if result['significant'] else 'Yes'}")

Real-World Example: Survey Analysis

class SurveyAnalyzer:
    def __init__(self, responses):
        self.data = np.array(responses)

    def test_independence(self, var1, var2):
        """Test if two variables are independent"""
        contingency = np.array([
            [sum((var1 == i) & (var2 == j))
             for j in set(var2)]
            for i in set(var1)
        ])

        chi2, p_val, _, _ = stats.chi2_contingency(contingency)

        return {
            'chi_square': chi2,
            'p_value': p_val,
            'related': p_val < 0.05
        }

# Example: Test if education level relates to job satisfaction
education = [1, 2, 2, 3, 2, 1, 3, 2, 2, 1]  # 1=HS, 2=College, 3=Graduate
satisfaction = [1, 2, 2, 3, 2, 1, 3, 2, 1, 1]  # 1=Low, 2=Med, 3=High

analyzer = SurveyAnalyzer(list(zip(education, satisfaction)))
result = analyzer.test_independence(education, satisfaction)

print(f"Related? {'Yes' if result['related'] else 'No'}")

When to Use

Independence Test
- Comparing categorical variables
- Testing relationships
- Survey analysis
Goodness of Fit
- Testing distributions
- Quality control
- Validating models

Key Points

Assumptions
- Independent observations
- Large enough sample
- Expected frequencies > 5
Interpretation
- Small p-value = significant relationship
- Large chi-square = stronger relationship
Limitations
- Only for categorical data
- Doesn’t show strength/direction
- Sensitive to sample size

Common Applications

def common_applications():
    return {
        'market_research': [
            'Brand preference vs age group',
            'Product choice vs income level'
        ],
        'quality_control': [
            'Defect patterns',
            'Process consistency'
        ],
        'medical_research': [
            'Treatment effectiveness',
            'Risk factor analysis'
        ]
    }

Remember: Chi-square tests help find patterns in categorical data but don’t tell you about the strength or direction of relationships.